The online version of this article (https://doi.org/10.18148/srm/8475) contains supplementary material.
It is a long-standing consensus among survey methodologists that response rates in surveys relying on probability samples of general populations have decreased over time, regardless of sampling design, survey mode, survey topic, or country (e.g., Atrostic et al., 2001; Battaglia et al., 2008; Bethlehem et al., 2011; Beullens et al., 2018; Brick, 2011, 2013; Curtin & Presser, 2005; Czajka & Beyer, 2016; de Heer, 1999; de Leeuw & de Heer, 2002; Dutwin & Lavrakas, 2016; Goyder & Leiper, 1985; Greaves et al., 2021; Groves & Cooper, 1998; Kreuter, 2013; Leeper, 2019; Rogers et al., 2004; Schnell, 1997; Singer, 2006; Stedman et al., 2019; Steeh, 1981; Steeh et al., 2001; Tourangeau & Plewes, 2013). In the case of probability samples, these decreasing response rates either lead to a loss of precision due to smaller sample sizes or a rise in survey costs due to the necessity to increase the gross sample. Beyond those immediate consequences, low response rates may also deteriorate surveys’ data quality through unit nonresponse bias; for brevity, the terms “nonresponse” and “nonresponse bias” are used to refer to unit nonresponse and unit nonresponse bias from here on.
It is, however, also known that low response rates do not necessarily translate into nonresponse bias. According to the formal definition of nonresponse bias, low response rates do not contribute to nonresponse bias if the covariance between the values of the target variable and the response probabilities in the population is zero (Bethlehem, 1988, eq. 3.5) Correspondingly, two older meta-analyses on the association between response rates and nonresponse bias (Groves, 2006; Groves & Peytcheva, 2008) found that survey nonresponse has not been a good indicator of the overall or average level of nonresponse bias at that time (Czajka & Beyer, 2016, p. 28). However, a more recent meta-analysis of 69 papers concluded that response rates are, in fact, negatively related to nonresponse bias (Cornesse & Bosnjak, 2018).
Despite these contradicting results, the increasing survey costs and the continuing decline in response rates have led pollsters and other survey practitioners to opt out of probability sampling (PSg) in favour of non-probability sampling (NPSg) with appropriate weighting (Cornesse et al., 2020). One key argument in favour of this change is that, with very low response rates, PSg does not lead to probability samples (PS) because the sampling probabilities are no longer known. In other words, PSg has become obsolete since we ended up in NPSg anyway (see, for example, Richter et al., n.d.). According to this view, one should start with NPSg and invest the cost savings into developing statistical countermeasures for selection biases.
The fear of unacceptable nonresponse bias caused by declining response rates is formally supported by the fact that the maximum possible unit nonresponse bias for a given variable monotonously increases with nonresponse (Bethlehem, 2010, p. 173). That is to say, the potential for nonresponse bias gets larger with decreasing response rates.
In this context, the present paper addresses the empirical question of whether and how the growing potential for nonresponse bias is realised. The key question is: Is there evidence for the feared decrease in sample quality due to nonresponse? To answer this question, we aim to estimate the total effects1 of historical time on nonresponse and nonresponse bias, as well as the contribution of nonresponse to nonresponse bias.
This study is distinct from previous studies on the association between nonresponse and nonresponse bias in several respects. To start with, the paper operationalises nonresponse bias in terms of an internal criterion of representativeness (Sodeur, 1997), while most other papers either use R‑indicators (Schouten et al., 2009; Schouten et al., 2011) or external benchmarks (Ortmanns & Schneider, 2016; Struminskaya et al., 2014; Yeager et al., 2011). Each approach to operationalise bias has its pros and cons (see Sect. 3.3), but one advantage of the internal criterion is that it can be easily calculated for many surveys without relying on strong assumptions or additional information beyond what is available in the survey dataset. The broad applicability of the internal criterion led to the creation of the survey metadata collection Sampling and Fieldwork Practices in Europe (SaFPE, Jabkowski, 2022; Jabkowski & Kołczyńska, 2020). The SaFPE contains comprehensive information on survey characteristics, response rates, and nonresponse bias measured relying on the internal criterion of representativeness of over 1500 European surveys conducted since the 1980s (see Sect. 3.1). It is a much larger dataset than any of the other compilations used in the previous studies with internal criteria (Eckman & Koch, 2019; Jabkowski & Cichocki, 2019; Kohler, 2007; Menold, 2014; Sodeur, 1997, 2007). The sheer size of this data allows us to study the evolution and associations of response rates and nonresponse bias in much more detail than before. It also adds a European perspective to the more frequently studied American cases. Most importantly, however, the SaFPE covers many countries, allowing statements about the heterogeneity of the associations between historical time, nonresponse rate, and nonresponse bias.
The SaFPE also allows for the study of the process that leads to nonresponse bias from a causal perspective. Aware of the obstacles to estimating causal parameters from observational data, we argue here that the presentation of statistical associations in the context of a clearly stated theoretical causal model eases the conceptual interpretation of the statistical results. To this end, we formalise our assumptions of the process leading to nonresponse bias with directed acyclic graphs (DAG; Pearl, 1994, 2009)2 and add to this the selection process of how surveys ended up in both the SaFPE and the subset being analysed. Using those DAGs, we formally derive adjustment sets for identifying the effects of historical time on nonresponse, and of both time and nonresponse on nonresponse bias.
The statistical analysis neither assumes the effects to be linear nor homogeneous. Instead, the distributions of effects are described using non-parametric techniques. Parametric linear mixed models are used to cross-check the results and perform formal tests of significance.
The paper is structured as follows. The next section presents the causal model of the process leading to nonresponse bias. Sect. 3 then describes the research design, starting with a presentation of the data (Sect. 3.1). The next subsection adds the data selection process to the model of the data generating process, followed by the derivation of the adjustment sets (Sect. 3.2). Subsects. 3.3 and 3.4 describe the operationalisations and statistical methods. Finally, Sect. 4 describes the results and Sect. 5 concludes.
We are aware that any attempt to estimate causal effects from observational data by means of covariate adjustment is a bold undertaking. Causal inference requires assumptions, and any estimates of causal effects are only valid to the extent that those assumptions are correct. Needless to say, the assumptions necessary for identifying causal effects by adjusting for observed covariates are often questionable. Many applied researchers react to this situation by stating that they are not interested in causal effects or that their estimates do not have a causal meaning (see, e.g., Kohler et al., 2023). However, the disadvantage of this forehandedness is that the actual interpretation of the results remains undefined, which makes the results immune to critique. We are convinced that striving for a well-defined research goal using explicitly disclosed assumptions will lead to a faster advance in knowledge (cf. Kohler et al., 2023; Lundberg et al., 2021; Pearl & Mackenzie, 2018, among many others). We invite researchers to use the SaFPE or other data to estimate the same parameters of interest using different assumptions.
The present paper strives to estimate the effects of time on nonresponse and nonresponse bias, and of nonresponse on nonresponse bias. Following Bethlehem (1988, p. 254)3, the nonresponse bias of the sample mean in a simple random sample is defined as:
with being the sample mean of some variable of interest, Y, and π is the individual probability to participate in the survey, given that the individual has been selected in the sample. Cov(·) is the covariance operator.
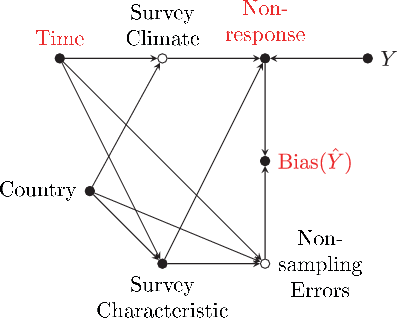
It follows from Eq. 1 that nonresponse bias has two major building blocks, the variable of interest Y, and the individual response probability π, which should thus become the major outcome variables for the assumed process creating bias. The assumptions underlying the analyses of this paper are shown through the directed acyclic graph (DAG) in Fig. 1.

The DAG includes all variables we assume to be relevant for the analysis; filled circles denote observed variables, and hollow circles denote unobserved variables. Following standard notation, the DAG uses arrows to show hypotheses on causal relations between the relevant variables. An arrow represents the hypothesis that there is at least one unit for which a change in the variable at the beginning of the arrow led to a change in the variable at the head of the arrow, even if any other variable remains unchanged (direct effect). It should be noted that the absence of an arrow between two variables encodes the assumption that there is no direct effect between them. The following justifies the causal assumptions encoded in the DAG and defines the parameters that answer the research question.
Nonresponse is considered to be partly a consequence of the variable Y, the survey climate (e.g., Brick & Williams, 2013; Gummer, 2019; Leeper, 2019), as well as survey characteristics such as survey mode (Atkeson et al., 2014; Daikeler et al., 2019; Dillman & Christian, 2005; Felderer et al., 2019; Lugtig et al., 2011; Manfreda et al., 2008; Tourangeau, 2017) and various other aspects of the implementation of the sampling design (e.g., Brick & Tourangeau, 2017; Cantor et al., 2008; Groves & Cooper, 1998; Groves & Heeringa, 2006; Laurie et al., 1999; Massey & Tourangeau, 2012; Pickery & Loosveldt, 2002; Schnell & Kreuter, 2000). The survey climate and survey characteristics are considered partly a consequence of historical time and country-specific circumstances.
Just like nonresponse, the variable of interest, Y, may also be affected by country and time. However, since we use the respondent’s sex as variable Y in our application (see Sect. 3.3), the corresponding arrows can be erased: the respondent’s sex would not change if it intervened on time and country. We also do not assume that Y is affected by any of the survey-specific variables (survey climate, survey characteristics, and nonresponse) since the causal model here is expressed in terms of the true values of Y and not of the measured indicator. We stress that the variable Y, like any other variable in the DAG, may be affected by additional idiosyncratic causes. Generally, some of these additional causes may also have direct effects on nonresponse, but for the particular case when Y is the respondent’s sex, it seems hard to think of a cause for sex that affects nonresponse not only through sex.
Following Eq. 1, the amount of bias in the mean of variable Y is affected directly by the overall amount of nonresponse, , and indirectly by Y through its association with π. However, the observed amount of bias, , might also be affected by nonsampling errors originating from time, country, and survey characteristics, which are thus added to the DAG.
Assuming this model of the data-generating process, the goal is to estimate (1) the total effects of historical time on nonresponse, (2) the total effect of time on nonresponse bias, and (3) the total effect of nonresponse on nonresponse bias. In addition to the general problem of identifying causal effects in observational data, it must be mentioned that we strive for the effects on the true values of the outcome variables. Thus, any associations originating from nonsampling errors should be removed from the associations between time, nonresponse and nonresponse bias. The analysis tries to accomplish these goals using adequate adjustment sets; see Sect. 3.2.
The analyses presented in this paper are based on a subset of the data collection Sampling and Fieldwork Practices in Europe (SaFPE), introduced in Jabkowski and Kołczyńska (2020) and since then updated with the most recent waves of all survey projects it covers. The SaFPE contains comprehensive information on the survey characteristics, response rates, and an internal criterion of representativeness of over 1500 European surveys conducted since the 1980s. From this resource, we use data describing surveys from four European survey projects, namely
the European Quality of Life Survey (EQLS 2018),
the European Social Survey (ESS 2002, 2004, 2006, 2008, 2010, 2012, 2014, 2016, 2018),
the International Social Survey Programme (ISSP 2002, 2003, 2009, 2012a, b, 2013a, b, 2015a, b, 2016a, b, 2017a, b, 2018a, b, 2019a, b, 2020, 2021),
whereby the records of the ISSP are limited to European countries. All four projects have established reputations and are commonly used in social science research. They are conceived as forward-looking, multi-wave endeavours enabling longitudinal and cross-country comparisons. All projects involve some degree of coordination aimed at within-project methodological consistency and comparability across national samples. They rely on samples designed to represent the entire adult populations of the respective country (with some differences in age cut-offs). Descriptions of the four projects are provided, e.g. in Jabkowski and Kołczyńska (2020). References to the specific datasets are listed in Appendix A.
The present analyses selected a subset of the SaFPE surveys using the following criteria:
The survey was carried out in 1999 or later. In surveys before 1999, either response rates or unit nonresponse bias were typically impossible to calculate. Moreover, the surveys from the early 1990s are only from ISSP, which was particularly poorly documented and relatively frequently used NPSg.
The sample was drawn using PSg. This excludes both surveys that used NPSg and surveys that are too poorly documented to determine whether or not they used PSGg. NPSg in surveys covered by the SaFPE are typically quota samples, where quotas on gender, by definition, affect our measure of unit nonresponse bias; see Sect. 3.3. Moreover, the concept of response rates cannot be easily applied to quota samples.
The survey did not allow substitutions. Substitution refers to the practice of replacing a unit nonresponse with a substitute unit during survey fieldwork (Vehovar, 1999). In practice, this often leads to substituting hard-to-reach or uncooperative respondents with easy-to-reach or cooperative respondents. Studies allowing substitutions are thus not considered to have probability sampling.
The harmonised response rate, defined as RR1 by the American Association for Public Opinion Research (2016), is calculable. This requires information on the number of completed interviews, refusals, noncontacts, ineligible cases, and cases of unknown eligibility; see Sect. 3.3.
Nonresponse bias in terms of the internal criterion is calculable, requiring information on sex, marital status, and household size; see Sect. 3.3.
Fig. 2 presents the consecutive steps of the subset selection process. The remaining dataset has records for 776 surveys. Table 1 provides basic information about the composition of the selected subset. We refer to this subset as the estimation sample in the following.
Table 1 Project characteristics
Project | Number of | Years | |||
Surveys | Countries | Waves | From | To | |
EQLS | 124 | 35 | 4 | 2003 | 2016 |
ESS | 231 | 37 | 9 | 2002 | 2018 |
EVS | 68 | 39 | 3 | 1999 | 2017 |
ISSP | 353 | 31 | 19 | 1999 | 2018 |
The described data selection process must be taken into account in order to identify the targeted causal parameters. Obviously, the surveys that ended up in the estimation sample have not been randomly chosen from the population of surveys in Europe. Thus, any causal parameter estimated from these selected data cannot be generalised to all European surveys or surveys in general. Instead, we suggest our results are only valid for the high-quality European probability-based surveys conducted between 1999 and 2020. Extrapolation beyond 2020 is challenging, as the COVID-19 pandemic rapidly changed the survey climate and many high-quality cross-national projects adapted their designs, moving away from face-to-face, interviewer-assisted surveys to pure self-completion modes of data collection. Nevertheless, the findings presented in this paper could be generalised to some other European probability sample surveys. For example, even though several longitudinal projects (e.g., Eurobarometer) and numerous one-year surveys were not included in this analysis because they do not provide information on survey response rates or other survey characteristics, we claim that the results can be generalised as long as the surveys follow the best methodological standards in sampling design and fieldwork implementation.4
As shown, some selection criteria for the study population are determined by the research design and thus limit the generalizability of the findings to European surveys with similar sampling designs and fieldwork implementation. However, the choice of countries at a particular time point within a cross-country project is not solely determined by those inclusion criteria. Particularly, some selection criteria also depend on the availability of corresponding information. The estimation sample includes data on four projects not because we a priori chose those projects by name but because other potentially suitable projects do not report the necessary information, such as response rates (e.g. the Eurobarometer). Within the projects, the inclusion of a given time-country combination depends on non-deterministic components such as financial viability, for example. Within the projects there are also variations-temporally and across countries, in the rigour with which they document sampling designs and fieldwork procedures. This divergence may result in a selective dropout of cases extending beyond the deterministic selection criteria. The DAG in Fig. 3 adds these additional processes to the assumed data-generating process of Fig. 1 above. We use this modified DAG for the definition of the adjustment sets in the next section.
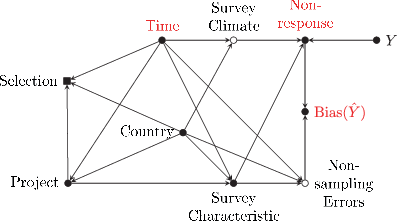
Fig. 3 Assumed data generating process, including the data selection process (Selection is a dummy variable with value of one, indicating that a survey is being selected into the estimation sample. Since the analysis can only be done with selected data, all analyses are conditioned upon the variable selection. This is highlighted by using a square symbol instead of a circle)
The paper strives to estimate the effects of time on both, nonresponse and nonresponse bias, and the effect of nonresponse on nonresponse bias. This subsection justifies the adjustment sets used to identify these effects. The adjustment sets are derived for each targeted effect from the DAG in Fig. 3. Appendix B provides the code to create the DAG of Fig. 3 on DAGitty5. Readers are invited to verify the statements made in this subsection there.
For the identification of the effect of time on nonresponse, it is necessary to observe that, in DAG terminology, conditioning on the variable selection d-connects (Elwert, 2013, p. 252) all the paths between the variables time and nonresponse running through selection. Thus, the observed bivariate association between time and nonresponse does not identify the requested effect, which would have been the case without the specific data selection process. Inspecting the DAG of Fig. 3 it becomes clear that no adjustment set fulfils the so-called adjustment criterion (see e.g. Elwert, 2013, p. 257). Four adjustment sets, however, request further discussion:
Empty set: In the estimation sample, bivariate associations are created by a broad mixture of causal and non-causal paths and are thus only of descriptive use.
Project only: Adjusting for project removes all biasing paths starting with “time → selection ← project” at the cost of adding several biasing paths starting with “time → project ← country”. It further creates an overcontrol bias by incorrectly removing two causal paths starting with “time → project → survey characteristic”. As there is little advantage in this model, again, it has only descriptive use.
Country only: This set removes any biasing paths starting with “time → selection ← country” but keeps two confounding paths starting with “time → selection ← project → survey characteristics.” Thus, the coefficient of this design is a biased estimate of the total effect to the extent of the association transported by those two paths.
Country and project: This set removes any of the confounding paths created by the data selection at the cost of blocking the same causal paths as adjustment set 1. Consequently, the estimated effect suffers from an overcontrol bias by the amount of the association transported by these causal paths.
We consider the adjustment set 4 as superior to the others since we consider the overcontrol bias to be very small.6 Some of the results will, therefore, only be presented for this adjustment set7, but the main results are presented for all 4 adjustment sets. If the estimated effects of time on nonresponse are similar for all adjustment sets, it corroborates the notion that the various biases are relatively small and thus strengthens the evidence that the estimated coefficients approximate the total effect.
The situation changes slightly for the effect of time on nonresponse bias. It has been argued above that the indicator for nonresponse bias could be affected by nonsampling errors. We have suggested that those nonsampling errors might originate from the country- and survey-specific circumstances and historical conditions. However, since we are interested in the effect of time on the true nonresponse bias, we must identify the causal effect of historical time net of the nonsampling errors. Inspecting the DAG of Fig. 3 it turns out that it is impossible to identify this effect without adjusting for nonsampling errors in Y. Since we do not have any indicator of nonsampling errors, the targeted causal effect of time on nonresponse bias remains unidentifiable through controlling for covariates.
However, there is perhaps a feasible identification strategy: If one is willing to assume that Y is measurable without nonsampling errors, the biasing paths through that variable would no longer exist. While such an assumption cannot be made in general, it might be less problematic in our particular case: Measurement error for sex in surveys we study is likely small, so the bias originating from paths through nonsampling errors may be considered small too.
After assuming the nonsampling errors away, the situation is identical to that of the effect of time on nonresponse: No adjustment set identifies the effect in question without biases, and the four adjustment sets suffer from the same biases. Thus, we again present the major findings for these four adjustment sets, while some results are only presented for results set 4. Results of analyses using the other response sets can be found in the Appendix C.
Given the assumptions of the data-generating process, the effect of nonresponse on nonresponse bias can be fully identified with two adjustment sets. These are:
Country, time, and survey characteristics;
Country, time, survey characteristics, and project.
Major results will be shown for both adjustment sets, while in some cases, we only show results for the more parsimonious adjustment set 1. We also add the empty set for descriptive purposes. If one is willing to assume that nonsampling errors are negligible for the case of sex, the bivariate association between nonresponse and nonresponse bias would also identify the total effect. In any case, if the result of all the adjustment sets were very similar, it would sustain the notion that nonsampling errors are negligible.
Whenever possible, the results of analyses using the other adjustment sets can be found in the Appendix C.
The following subsection describes the operationalisation of all variables used in the analysis. It is structured by the names of the variables used in Fig. 3. Survey climate and nonsampling errors remain unmeasured, survey characteristics are measured by multiple indicators, and the operationalisation of nonresponse bias sets the variable Y by definition.
The literature distinguishes two main approaches to evaluating sample representativeness. The first includes indicators based on response propensities among respondents and non-respondents, such as R‑indicators (Schouten et al., 2009; Schouten et al., 2011) and balance indicators (Lundquist & Särndal, 2013; Särndal, 2011). Applying methods from this group requires valid information about non-respondents or response rates in different population groups, which almost unavoidably limits the number of comparable surveys. Consequently, papers using R‑Indicators to study correlates of nonresponse bias do so for only a small or moderate number of surveys. Cornesse and Bosnjak (2018), for example, listed ten peer-reviewed papers using R‑indicators to study the representativeness of one (Roberts et al., 2014) to 36 (Bańkowska et al., 2015) surveys. The average number of surveys in those papers was 6.8.
The second group includes methods that do not require information about non-respondents, comprising two main approaches. The first involves comparing the composition of the achieved sample to the composition of the target population. For our analysis, this approach has certain drawbacks. First, the results of applying this approach may be affected by coverage error (Biemer & Lyberg, 2003, p. 63). Second, if the external benchmark data come from (high-quality) surveys (e.g., the European Labor Force Survey) instead of the census, the results may also suffer from representation and measurement errors. Third, external criteria methods critically rely on the availability of design weights in surveys that use complex sampling strategies (Jabkowski et al., 2021). Fourth, and most importantly, the technique requires comparable valid information from both the achieved sample and the target population, which strongly limits the applicability of the approach. In fact, the usage of an external benchmark is typically done for just one sample. A notable exception is Yeager et al. (2011) who compared the marginal distribution of selected variables of nine surveys with corresponding benchmarks from administrative records and high-quality surveys.
The second approach, not requiring information on non-respondents, relies on the so-called internal criteria of representativeness (Sodeur, 1997). The general idea is to find a sub-group in the achieved sample for which the true value of a statistic is known by definition. The difference between this true value and the observed statistic can then be taken as an indicator of the nonresponse bias. Leaving measurement error aside, this is because any significant deviation of the observed and true values originates from unit nonresponse (Kohler, 2007, p. 59): First, because unit nonresponse directly leads to bias if some members of the subgroup more often reject requests to participate in a survey than others. Second, because a refusal to participate may create interviewer, or respondent misbehaviour, which in turn leads to bias as well. An example of this second reason is when a target person’s refusal leads the interviewer to substitute the target person with another person in the same household or neighbourhood. The same applies if the target respondent in a self-administered survey mode refuses to participate in the survey and asks someone else in the household to participate.
The most frequently used variant of the internal criteria approach exploits the fact that in the population of two-person households inhabited by heterosexual couples, the proportion of women is known to be 0.5 (Eckman & Koch, 2019; Jabkowski & Cichocki, 2019; Kohler, 2007; Menold, 2014). Comparing the proportion of women in the subset of such two-person households with 0.5 gives us a measure of unit nonresponse bias, which we define for survey i as:
where is the observed proportion of women in the subsample of two-person households inhabited by heterosexual couples, and 0.5 is the corresponding true proportion in that population. The denominator is the standard error of the difference in the nominator. Hence, an absolute bias beyond 1.96 is considered to exceed conventional thresholds of random fluctuation.
Before presenting the distribution of the unit nonresponse bias in the SaFPE collection, three possible shortcomings of the measure need to be discussed:
For the case of multi stage samples based on individual registers, persons within a two-person household may have different probabilities of being selected into the sample, which would invalidate the 0.5 benchmark. This may happen if respondents of different sexes have different selection probabilities by design, either through the oversampling of one of the sexes or through oversampling by another characteristic that happens to be correlated with sex. We claim this issue does not meaningfully affect our data. First, among the surveys we analysed, none used oversampling by sex. Second, in surveys that provide design weights that would correct for the unequal selection probabilities between men and women, the consequence of omitting design weights when calculating nonresponse bias is small, as shown in Jabkowski, Cichocki, and Kołczyńska (2021). Third, multi stage samples with individual registers constitute a minority of the samples in our analysis. Most surveys use either address or household-register samples, listing or random route samples, or simple random samples, for which design weights can be ignored (Jabkowski et al., 2021).
The approach does not consider heterosexual couples. Only two of the four projects analysed here (ESS and EQLS) collect complete household grids to enable filtering out homosexual couples. EVS and ISSP only provide information about the respondent’s sex, marital status, and household size (the ESS and EQLS also provide this information). Hence, to select the respondent subset in the same way in all four projects, we use an approximate definition and select respondents who are married or in a civil partnership and living in two-person households. Without knowing the sex of the other household member, the resulting measure is prone to bias if marriage among same-sex couples is more frequent for one sex than for the other. Although it can be expected that the number of same-sex couples has increased over time, available survey data do not suggest that cohabitation behaviour differs strongly between female and male homosexuals. According to data from the ESS rounds 1–9 and EQLS rounds 1–4, the share of married samesex couples in the sub-sample of married couples accounts for around 2% in the ESS and 3% in EQLS. In both projects, women constitute about 40% of two-person households of married same-sex couples. Consequently, the correlation between an estimate of unit nonresponse bias with and without exclusion of same-sex couples is close to 1.
If citizens of one sex more frequently marry noncitizens of the other sex, the true share of women among two-person married couples in a sample of citizens would also deviate from 0.5. However, a review of the survey documentation of the analysed projects shows that the target population definitions do not include the nationality or citizenship criterion (Jabkowski & Kołczyńska, 2020).
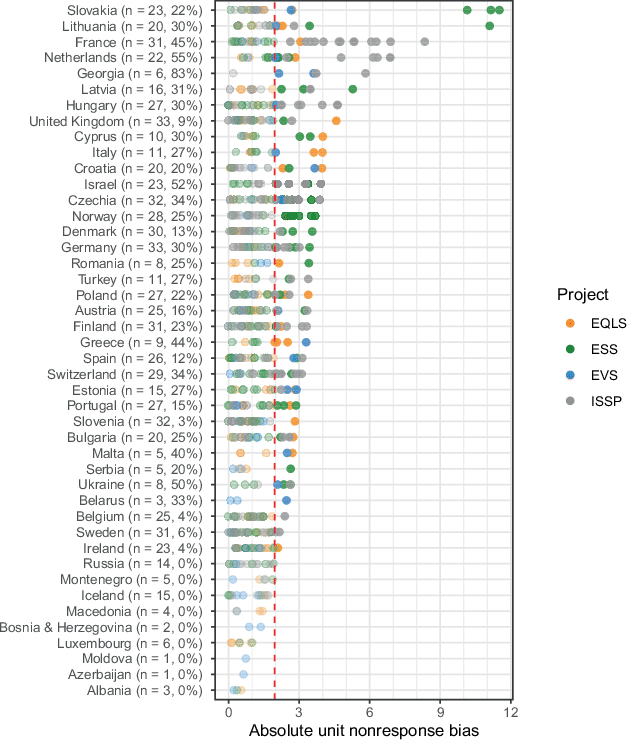
Fig. 4 shows the distributions of nonresponse bias in all selected surveys across the four projects. Despite being quite similar, EVS has the lowest median bias of 0.9, followed by EQLS (1.0), ISSP (1.1) and ESS (1.1). The proportion of surveys with absolute bias exceeding 1.96 varies slightly across projects but is substantially larger than the 5% that could be expected by pure chance. Specifically, the proportion of significant deviations from the true value ranges between 20% in the ESS, 22% in the EQLS, up to 24% in the ISSP and 25% in the EVS. The graph also shows four surveys with extremely high unit nonresponse bias above 10, which all belong to the ESS, and a group of surveys with very high bias above 5 in the ISSP. Overall, bias varies in a way that requires an explanation, and low response rates are certainly one candidate for it.
Fig. 5 shows absolute bias by country, with each point representing one survey, the colour indicating the project the survey belongs to, and the dashed line marking the 1.96 threshold. Countries are sorted according to declining maximum values of absolute bias. As already mentioned, the most extreme outliers are in the ESS. The ranking is led by Slovakia, whose three biased samples are address-based after earlier waves used an individual register (Jabkowski et al., 2021). We find no obvious explanation for the single extremely biased survey from Lithuania in ESS Round 98. Next come countries with multiple strongly biased surveys in the ISSP, such as France and the Netherlands, where the high bias is likely due to the self-administered mode used by these surveys. Overall, most countries have at least some excessively biased surveys. Exceptions include countries that have conducted very few surveys. Of the frequently surveyed countries (with more than five surveys), Iceland, Russia, and Luxembourg stand out for the lack of biased surveys. It is worth noting that this comparison does not represent the assessment of the overall survey quality across countries, given that our data subset excludes surveys with NPSg, poorly documented surveys, and surveys which allow for substitutions.
For all selected surveys, the SaFPE contains harmonised response rates calculated following the first version of the AAPOR’s standard definition (American Association for Public Opinion Research, 2016). The harmonised response rate is preferred to the response rates reported by data providers since they lack comparability due to different definitions. Distributions of harmonised response rates by project are presented in Fig. 6. Response rates are highest on average in the ESS, with the median at 60% and a relatively small variance. In the EVS, the median is slightly lower (57%), followed by the ISSP (51%) and the EQLS (47%).
Before describing the specific operationalisation of survey characteristics, it must be noted that the variation of the survey characteristics is already limited by the selection of surveys: all surveys selected respondents with a PSg design that does not allow for substitutions. Moreover, all surveys belong to survey projects that prescribe specific standards in implementation, including quality checks of interviews. Hence, even in adjustment sets that do not include survey characteristics, some aspects of survey characteristics are still controlled for. At the same time, the adjustment of survey characteristics in those cases where survey characteristics must be controlled for is more complete than it looks at first sight.
In addition to restricting the analysis to specific surveys, some adjustment sets use the sample type, fieldwork duration, and survey mode.
The sample types of the examined surveys were grouped into three types:
individual register samples (single- and multistage),
household register samples,
area sampling (incl. random route).
This classification is similar to that used by Kohler (2007). However, it does not differentiate between single- and multistage individual-register samples, and it excludes surveys that used NPSg and surveys with insufficient information on the sampling design since these surveys have been removed from the estimation sample from the start. In the selected subset, there are 302 individual register samples, 347 household register samples, and 127 area samples (incl. random route samples); see Table 2.
Table 2 Distribution of sample types across projects
Project | Individual register | Household register | Area samples | Total |
EQLS | 10 | 33 | 81 | 124 |
ESS | 111 | 103 | 17 | 231 |
EVS | 24 | 22 | 22 | 68 |
ISSP | 157 | 189 | 7 | 353 |
Total | 302 | 347 | 127 | 776 |
Fieldwork duration is measured as the period between the start and the end of the fieldwork period. In cases where only fieldwork months are provided, the first day of the month is used as the start and the last day of the month as the end of the fieldwork period. On average, fieldwork duration is the shortest in EQLS (75 days), followed by ISSP (96 days), EVS (108 days), and ESS (132 days). To avoid very small coefficients, fieldwork length is expressed in hundreds of days. Fig. 7 shows the distributions of fieldwork length by project.
The survey mode distinguishes between surveys administered via face-to-face interviews (either paper-and-pencil or computer-assisted) or other modes, including computer-assisted telephone interviews, computer-assisted web interviews, postal surveys and self-completion surveys. Table 3 presents the distribution of modes across projects.
Table 3 Distribution of survey modes across projects
Project | F2F | Not F2F | Total |
EQLS | 124 | 0 | 124 |
ESS | 231 | 0 | 231 |
EVS | 67 | 1 | 68 |
ISSP | 237 | 116 | 353 |
Total | 659 | 117 | 776 |
Based on the information about the start and end of fieldwork used to calculate fieldwork length, we also calculated the mid-point of fieldwork, represented as a decimal. We use it as the measure of the time of fieldwork.
The project within which a given survey was conducted is identified through a nominal scaled categorical variable (EQLS, ESS, EVS, and ISSP).
Country is measured as a nominal scaled variable. The response rates and nonresponse bias were calculated for the entire country whenever the survey was conducted separately in sub-national units, e.g., in (former) East and West Germany.
Two strategies are used to estimate the effects of interest. The first strategy shows the effects graphically with non-parametric regression lines (LOESS; see Cleveland et al., 1992). The adjustment of covariates is made by showing the results separately by project and by identifying observations from the same country. This mimics an adjustment set containing country and project, which is one of the four adjustment sets for the analysis of the effects of time on nonresponse and time on nonresponse bias and a major building block of the adjustment sets for the identification of the effect of nonresponse on nonresponse bias (cf. Sect. 3.2).
The second approach uses regression models of the outcome variable on the exposure variable, adjusting for the corresponding adjustment sets. We use two techniques: linear mixed models and two-step multi-level modelling (Achen, 2005). The mixed models use the country to define the random intercept and random slopes for selected variables. For the two-step approach, all the models are estimated separately for each country. In both cases, the other variables from the adjustment sets were controlled for by adding them as covariates in the corresponding regression.
The following documents the equations for the mixed and by-country models for each of the three research questions.
The mixed model to estimate the effect of time on the response rate is estimated with the regression:
where RR is the response rate, T is time and A is one of the adjustment sets defined in Sect. 3.2. β0 is the grand intercept; v0i is the country random intercept; β1 is the coefficient for time; v1i is the random slope for time, allowed to vary across countries; γ represents coefficients for the adjustment variables; and ϵitp is the residual varying by country i, time t and project p.
The by-country model is:
with all variables and parameters defined as above. Note that in this case, there are as many coefficients of β as there are countries. For the sake of brevity, we only present results for adjustment set 4 (country and project), which has been described as superior to the other adjustment sets above9. Results for the remaining adjustment sets are available in Appendix C.
For estimating the effect of time on nonresponse bias, the mixed models have the form
and the by-country models are defined as
where Bias is the absolute unit nonresponse bias as defined in Sect. 3.3. All the other terms are defined as above. Again, we present results of the by-country model only for the adjustment set consisting of country and project. Results for the remaining adjustment sets are available in Appendix C.
For estimating the effect of response rates on nonresponse bias, the mixed model is:
and the by-country models are:
We present results for the by-country models only for the adjustment set, consisting of country, time and survey characteristics. Results for the remaining adjustment sets are available in Appendix C.
This section describes the results of the analytical questions asked in the introduction. The first part of the analysis shows that overall response rates decreased over time and control for the proposed adjustment sets. The second part demonstrates that nonresponse bias remained relatively stable throughout the analysed period despite decreasing response rates, again both overall and controlling for the identified adjustment sets. The final part shows that unit nonresponse bias is not affected by nonresponse.
Fig. 8 shows a non-parametric approach to studying the effects of time on response rate adjusted for project and country (adjustment set 4). To this end, the figure plots harmonised response rates over time for each project separately. Each point corresponds to one survey, and surveys from the same country are connected with a line. The lines make it possible to trace changes by country within the project, which essentially means to adjust the analysis to country and project.
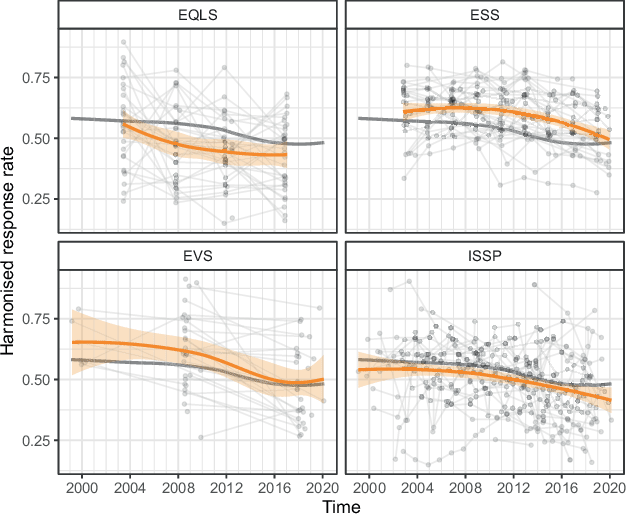
While in the EQLS, ESS, and EVS, most countries have declining trajectories in response rates, in the ISSP, some zigzags are evident, which could be related to the fact that the ISSP is often conducted together as with (typically, following) another survey, so it is often unclear what the response rates exactly represent.
The overlaid orange lines show locally estimated smoothing trends for surveys of the projects together with 95% confidence intervals (Cleveland et al., 1992). To ease the comparison between projects, we also show the overall trend for all surveys included in the analysis (Figure 8).
Table 4 Effects of time on response rates
Adjustment set | Coef | S.E. |
See Appendix C1 for full results a Without random intercept/coefficients for country * | ||
Empty seta | −0.007* | 0.001 |
Projecta | −0.007* | 0.001 |
Country | −0.007* | 0.002 |
Country, project | −0.008* | 0.002 |
Number of surveys | 774 | |
Number of countries | 42 | |
Overall, and for each project, there is a declining trend in response rates. Due to the large variance in the response rates, the trend looks relatively modest in the graph. However, it must still be considered quite substantial. Comparing the start and the end of the smoothed trend lines in EQLS, the average response rates decreased from around 56% in the first wave in 2003 to 43% in the most recent wave in 2016. In the ESS, the response rates decreased from 61 to 51%, for EVS from 65% in the 1999 wave to 49% in the 2017 wave, and for ISSP from 54% in the 1999 wave to 43% in wave 2018. Such a decrease could substantially increase unit nonresponse bias, especially for heterogeneous characteristics. The latter can be illustrated using Bethlehem’s formula for unit nonresponse bias in simple random samples (Eq. 1, above; see Bethlehem, 1988, Eq. 3.5): For a uniformly distributed dichotomous variable that correlates only weakly (which according to Cohen, 1988 corresponds to a correlation of ) with nonresponse, the expected nonresponse bias for the EQLS would increase from around 4 to almost 6%.
In order to more formally examine the effect of time on the response rates, Table 4 presents the results of the mixed models following Eq. 3 using the four adjustment sets derived in Sect. 3.2.10
Table 5 Effects of time on nonresponse bias
Adjustment set | Coef | S.E. |
See Appendix C2 for full results a Without random intercept/coefficients for country * | ||
Empty seta | −0.002 | 0.009 |
Projecta | −0.002 | 0.009 |
Country | −0.006 | 0.009 |
Country, project | −0.006 | 0.009 |
Number of surveys | 774 | |
Number of countries | 42 | |
The average effect of time in all models is negative and significant (), as expected. The results of the four models are very similar, varying between −0.007 for adjustment sets 1, 2, and 3 to −0.008 in the fourth model. Over ten years, this average estimated effect would accumulate into a noticeable amount of around 7–8 percentage points. The small variance between the models corroborates the notion that the various biasing path effects are rather small.
The distribution of country slopes from the model using the fourth adjustment set is presented in the upper panel of Fig. 9. It shows that in 83% of countries (35 out of 42), the slopes are negative. The lower panel of the figure shows in comparison the effects of time in the equivalent by-country models following Eq. 5. The distribution of slopes clearly confirms the domination of the negative effects of time on response rates.
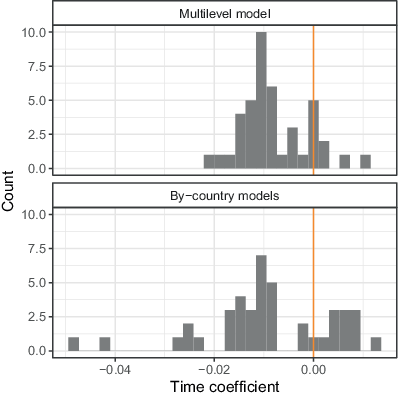
Overall, the analyses clearly sustain the well-established finding of decreasing response rates also for top-quality surveys of the estimation sample. Thus, the potential for nonresponse bias has substantially increased over time. The next section analyses whether there has been, in fact, an increase of nonresponse bias over time.
Fig. 10 presents the non-parametric approach to analyzing absolute unit nonresponse bias. As before, the symbols representing surveys from one country and project are connected with a line, which mimics an analysis that is adjusted for the country and project. It must be noted that surveys with absolute bias exceeding 4.6, representing the top 3% of biased surveys, have been removed from the scatter plot but not from the estimation of the LOESS curves. A version of the plot with all the outliers is shown in Figure E1 in Appendix E.
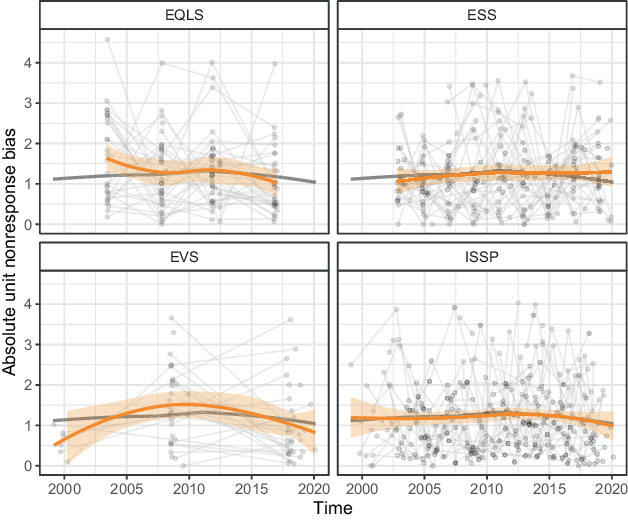
Fig. 10 Absolute nonresponse bias over time by project (The grey curve indicates the LOESS trend in all surveys in the estimation sample. The orange curves indicate the LOESS trends within each project, with the 95% confidence interval indicated by the ribbon. Y-axes corresponding to nonresponse bias are restricted to exclude outliers with bias exceeding 4.6 to improve readability. LOESS curves are calculated with all observations)
The figure does not show any clear association between time and nonresponse bias. Neither the overall nor project-specific time trends nor the country-specific lines show any visible tendency that the higher leverage for nonresponse bias has been used. The following checks if this result also holds when using other adjustment sets.
Table 5 presents the four models following Eq. 5, one for each of the adjustment sets listed in Sect. 3.2. In none of the models is the effect of time on nonresponse bias statistically significant at the customary levels of . More importantly, the coefficients of all four models are negative, meaning that the nonresponse bias, on average, has not increased but decreased over time. The effects are, however, very small. Over ten years, the effect of time would accumulate to a decrease in nonresponse bias by 0.02–0.06. Given that the observed range of nonresponse bias in our data is between 0 and 11.5 we consider this change as negligible and conclude that nonresponse bias has not changed over time.
Fig. 11 shows the distribution of the estimated time slopes of the mixed and by-country models with the fourth adjustment set (country and project). In the mixed models, 12 slopes are positive, and 30 are negative, but all are relatively small and fall in the range between −0.03 and 0.007. Over ten years, the estimated change in nonresponse bias would be between −0.3 and +0.07, which is still relatively modest given our bias indicator’s range. The results of the by-country models overall further support this conclusion. Although some countries have substantial increases or decreases in nonresponse bias, there are around as many positive results (18) as negative results (24). Such a distribution of positive and negative coefficients would be very likely under an assumption of no effect of time. In fact, the probability to observe 18 or fewer positive results out of 42 is almost 1 if the probability of positive results would be 0.5.
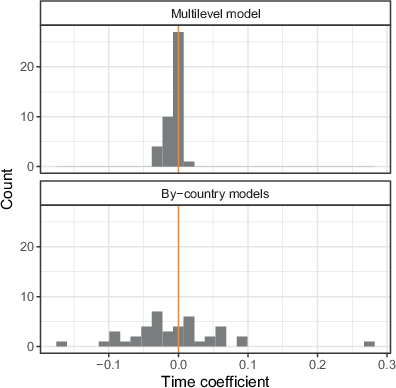
Overall, the analyses do not show any indication that nonresponse bias has systematically increased over time. In that sense, the growing potential for biased results from increased response rates has not materialised. We stress, however, that results shown in Appendix E indicate that surveys with outstandingly high nonresponse biases may have become a bit more frequent over time. However, the number of such cases is too low to affect the overall associations and make a decisive statement.
The previous subsections showed that response rates have declined over time, while nonresponse bias does not reveal any signs of increasing. These results already place a question mark on the expectation that decreased response rates deteriorate the quality of results from probability samples. The following subsection studies this effect directly.
Fig. 12 shows the non-parametric approach to studying the effects of response rates on nonresponse bias in the same way as before. It should be mentioned here that in this case, none of the adjustment sets derived in Subsect. 3.2 adjusted for project and country. The analysis presented here is, therefore, only an estimate of the total effect of response rate on nonresponse bias if one is willing to assume that nonsampling errors are negligible for the case of the measurement of sex.
Having offered this word of caution, the graphs do not show a clear pattern in the association between nonresponse bias and nonresponse. If anything, we find increasing biases with increasing response rates for two survey projects (EQLS and ISSP) and decreasing biases with increasing response rates for the other two (ESS and EVS). In either case, there is huge country variation within each project and some indication that the overall rise or decline of the unit nonresponse bias is predominantly associated with surveys with very high response rates (above 75%). Thus, we read the graph as showing no clear association between nonresponse bias and response rate.
Table 6 shows the results of the mixed models following Eq. 7 and using the adjustment sets defined in Sect. 3.2. The coefficient of nonresponse of the model using the empty set can only be considered an estimate of the total effect if one is willing to accept the assumption of negligible nonsampling errors in the measurement of sex.
Table 6 Models estimating the effect of response rate on nonresponse bias
Adjustment set | Coef | S.E. |
See Appendix C3 for full results a Without random intercept/coefficients for country * | ||
Time, survey characteristics | 0.298 | 0.621 |
Time, project, survey characteristics | 0.099 | 0.641 |
Empty seta | −0.409 | 0.331 |
Number of surveys | 774 | |
Number of countries | 42 | |
The results, presented in Table 6, reveal no significant impact of response rates on the absolute bias. Concentrating on the more trustworthy estimates of the total effects from the first two models, the effects also have the opposite sign than expected under the “declining response rates hurt sample representativeness” hypothesis: A positive coefficient means that higher response rates translate into more bias, not less. Only the effect of the model without adjustment of covariates is negative. Moreover, all coefficients are substantively very small: remember that they represent an effect on absolute nonresponse bias (which in our analytical dataset ranges from 0 to 11.5) of a change in response rates from 0–100%.
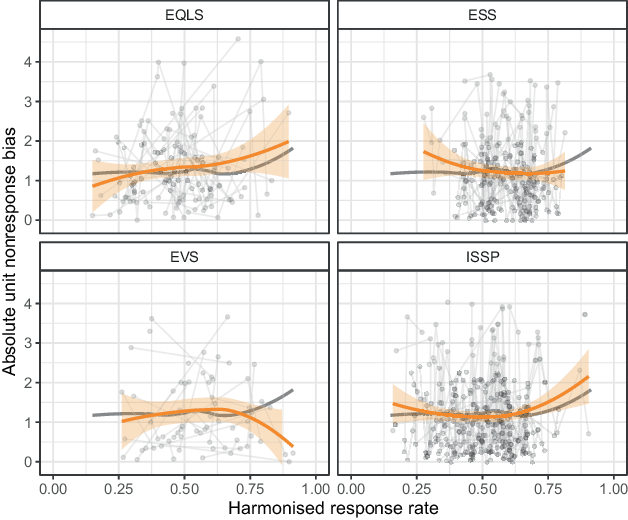
Fig. 12 Absolute nonresponse bias and response rates by project (The grey curve indicates the LOESS trend in all surveys in the estimation sample. The orange curves indicate the LOESS trends within each project, with the 95% confidence interval indicated by the ribbon. Y‑axes corresponding to nonresponse bias are restricted to exclude outliers with bias exceeding 4.6 to improve readability. LOESS curves are calculated with all observations)
Fig. 13 shows the distribution of response rate effects from the mixed and by-country models adjusting for country and survey characteristics (adjustment set 1). The mixed model results reveal a positive association for 25 countries and a negative association for all the others. Such a distribution is highly probable under the assumption that there is no effect, so the coefficient’s sign is just like flipping a coin. The same is true for the results of the by-country models, where 24 slopes are positive, and 18 are negative. In the by-country models, some countries show substantial effects, though, primarily because for these countries only very few surveys are available, leading to extreme coefficient values.
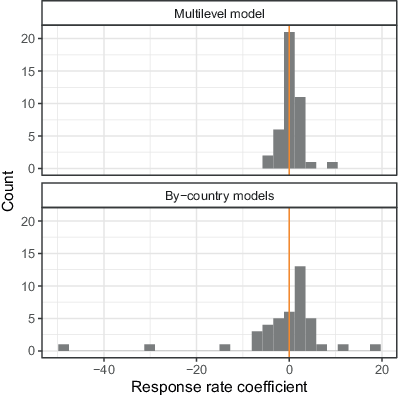
The analysis in this subsection does not reveal any evidence that decreasing response rates deteriorated the survey quality in terms of unit nonresponse bias. Overall, the effect of nonresponse is opposite to standard whispering, but in any case, the effect is very small, uncertain and also not statistically significant.
The present paper asked whether increases in nonresponse rates observed in European social science surveys translated into an increase in nonresponse bias of survey samples. Based on the data from almost 800 surveys carried out in Europe in the last two decades and clearly stated assumptions of the data-generating process, the answer is “no”. More specifically, there was an evident rise in nonresponse in the last two decades, but there was no parallel increase in nonresponse bias. Correspondingly, there is no observable effect of nonresponse on nonresponse bias. If anything, on average and in the majority of countries from which we have data, the estimated coefficients of response rates on bias are even positive, not negative.
Based on these results, the argument that declining response rates challenge the applicability of PSg seems invalid. The data that arose from PSg, as implemented in the social sciences, have shown an astonishing robustness against the threats of decreasing response rates. In that sense, PSg has not become obsolete!
The result that decreasing response rates did not lead to decreasing survey quality does not mean that response rates are irrelevant. Of course, increasing nonresponse creates a potential for nonresponse bias. But at least in high-quality surveys such as those analysed here, the potential does not materialise. Either nonresponse is predominantly driven by the presumably random situation in which the target respondent is approached (Dalenius, 1983, p. 412), or the stable characteristics are uncorrelated with sex, or the measures the survey institutes to counteract systematic nonresponse have been successful.
The present study naturally has limitations. First, results may apply only to high-quality surveys where substantial effort and methodological expertise are employed to meet quality standards. The effect of nonresponse on nonresponse bias may well be different in public opinion polls, in which data are often collected under considerable time pressure. Second, in the surveys we analysed, response rates on average were not low. It is unclear whether the results hold also for surveys with very low response rates. Third, it is possible that in high-quality surveys, such as the ones we analysed, the decline in response rates was compensated by increased effort, e.g. interviewer supervision (e.g., with GPS and interview recording) and overall quality control investments, which we do not measure and hence cannot adjust for. Finally, the measure of nonresponse bias used here has advantages, which were discussed, but it is also inherently limited by being based on the subset of two-person households with heterosexual couples and referring to sex only. The results would be worth replicating with other measures of nonresponse bias, ideally with a large-scale study such as the present one.
We note that the analysis was only possible thanks to the survey documentation made available by the survey projects, which included, for all or at least a vast majority of surveys, response rates (or information necessary to calculate them), information about the sample type and fieldwork duration, among the many different kinds of information these projects document. Publicly available, high-quality survey documentation is necessary to evaluate survey quality by secondary data users and should be the standard for publicly funded surveys (we are looking at you, Eurobarometer!). Publishing additional information, e.g., about non-respondents, would enable replicating the results at scale with other measures of bias.
Achen, C. (2005). Two-step hierarchical estimation: beyond regression analysis. Political Analysis, 13, 447–456. https://doi.org/10.1093/pan/mpi033 →
American Association for Public Opinion Research (2016). Standard definitions: final dispositions of case codes and outcome rates for surveys. 9th edition. https://www.aapor.org/AAPOR_Main/media/publications/Standard-Definitions20169theditionfinal.pdf a, b
Atkeson, L. R., Adams, A. N., & Alvarez, R. M. (2014). Nonresponse and mode effects in self- and intervieweradministered surveys. Political Analysis, 22(3), 304–320. https://doi.org/10.1093/pan/mpt049. →
Atrostic, B. K., Bates, N., Burt, G., & Silberstein, A. (2001). Nonresponse in U.S. government household surveys: consistent measures, recent trends, and new insights. Journal of Official Statistics, 17(2), 209–226. →
Bańkowska, K., Osiewicz, M., & Pérez-Duarte, S. (2015). Measuring nonresponse bias in a cross-country enterprise survey. Austrian Journal of Statistics, 44(2), 13–30. https://doi.org/10.17713/ajs.v44i2.60. →
Battaglia, M. P., Khare, M., Frankel, M. R., Murray, M. C., Buckley, P., & Peritz, S. (2008). Response rates: how have they changed and where are they headed? In Advances in telephone survey methodology (pp. 529–560). Hoboken: Wiley. →
Bethlehem, J. (1988). Reduction of nonresponse bias through regression estimation. Journal of Official Statistics, 4(3), 251–260. a, b, c
Bethlehem, J. (2010). Selection bias in web surveys. International Statistical Review, 78(2), 161–188. https://doi.org/10.1111/j.1751-5823.2010.00112.x. →
Bethlehem, J., Cobben, F., & Schouten, B. (2011). Handbook of nonresponse in household surveys. Hoboken: Wiley. →
Beullens, K., Loosveldt, G., Vandenplas, C., & Stoop, I. (2018). Response rates in the european social survey: increasing, decreasing, or a matter of fieldwork efforts? Survey methods: insights from the field, Vol. 9673. https://doi.org/10.13094/SMIF-2018-00003 →
Biemer, P., & Lyberg, L. E. (2003). Introduction to survey quality. Hoboken: Wiley. →
Bradley, V. C., Kuriwaki, S., Isakov, M., Sejdinovic, D., Meng, X.-L., & Flaxman, S. (2021). Unrepresentative big surveys significantly overestimated US vaccine uptake. Nature, 600(7890), 695–700. https://doi.org/10.1038/s41586-021-04198-4. →
Brick, J. M. (2011). The future of survey sampling. Public Opinion Quarterly, 75(5), 872–888. https://doi.org/10.1093/poq/nfr045. →
Brick, J. M. (2013). Unit nonresponse and weighting adjustments: a critical review. Journal of Official Statistics, 29(3), 329–353. https://doi.org/10.2478/jos-2013-0026. →
Brick, J. M., & Tourangeau, R. (2017). Responsive survey designs for reducing nonresponse bias. Journal of Official Statistics 33(3), 735-752. https://doi.org/10.1515/jos-2017-0034. →
Brick, J. M., & Williams, D. (2013). Explaining rising nonresponse rates in cross-sectional surveys. The Annals of the American Academy of Political and Social Science, 645(1), 36–59. https://doi.org/10.1177/0002716212456834 →
Cantor, D., O’Hare, B. C., & O’Connor, K. S. (2008). The use of monetary incentives to reduce nonresponse in random digit dial telephone surveys. In J. Lepkowski, C. Tucker, J. M. Brick, E. D. de Leeuw, L. Japec, P. J. Lavrakas, M. W. Link & R. L. Sangster (Eds.), Advances in telephone survey methodology. Hoboken: Wiley. →
Cleveland, W. S., Grosse, E., & Shyu, W. M. (1992). Local regression models. In J. M. Chambers & T. J. Hastie (Eds.), Statistical Models in S (pp. 309–376). Belmont: Wadsworth & Brooks/Cole. a, b
Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Mahwah: Erlbaum. →
Cornesse, C., & Bosnjak, M. (2018). Is there an association between survey characteristics and representativeness? A meta-analysis. Survey Research Methods, 12(1), 1–13. https://doi.org/10.18148/srm/2018.v12i1.7205. a, b
Cornesse, C., Blom, A. G., Dutwin, D., Krosnick, J. A., de Leeuw, E. D., Legleye, S., Pasek, J., Pennay, D., Phillips, B., Sakshaug, J. W., Struminskaya, B., & Wenz, A. (2020). A review of conceptual approaches and empirical evidence on probability and nonprobability sample survey research. Journal of Survey Statistics and Methodology, 8(1), 4–36. https://doi.org/10.1093/jssam/smz041. →
Curtin, R., Presser, S., & Singer, E. (2005). Changes in telephone survey nonresponse over the past quarter century. Public Opinion Quarterly, 69(1), 87–98. https://doi.org/10.1093/poq/nfi002 →
Czajka, J. L., & Beyer, A. (2016). Declining response rates in federal surveys: trends and implications. Paper submitted to the Office of the Assistant Secretary for Planning and Evaluation, U.S. Department of Health & Human Services by Mathematica Policy Research. https://aspe.hhs.gov/sites/default/files/private/pdf/255531/Decliningresponserates.pdf a, b
Daikeler, J., Bosnjak, M., & Lozar Manfreda, K. (2019). Web versus other survey modes: an updated and extended meta-analysis comparing response rates. Journal of Survey Statistics and Methodology, 8(3), 513–539. https://doi.org/10.1093/jssam/smz008. →
Dalenius, T. (1983). Some reflections on the problem of missing data. In Incomplete data in sample surveys (Vol. 3, pp. 411–413). New York, Boston, London, Oxford: Academic Press. →
Dillman, D. A., & Christian, L. M. (2005). Survey mode as a source of instability in responses across surveys. Field Methods, 17;(1), 432–435. https://doi.org/10.1177/1525822X04269550 →
Dutwin, D., & Lavrakas, P. (2016). Trends in telephone outcomes, 2008–2015. Survey Practice, 9(3), 1–6. https://doi.org/10.29115/SP-2016-0017 →
Eckman, S., & Koch, A. (2019). Interviewer involvement in sample selection shapes the relationship between response rates and data quality. Public Opinion Quarterly, 83(2), 313–337. https://doi.org/10.1093/poq/nfz012. a, b
Elwert, F. (2013). Graphical causal models. In S. Morgan (Ed.), Handbook of causal analysis for social research (pp. 245–273). Dordrecht: Springer. a, b, c
European Foundation for the Improvement of Living and Working Condition (2018). European Quality of Life Survey integrated data file, 2003–2016. https://doi.org/10.5255/UKDA-SN-7348-3. →
European Social Survey (2002). European social survey round 1 data. https://doi.org/10.21338/NSD-ESS1-2002. →
European Social Survey (2004). European social survey round 2 data. https://doi.org/10.21338/NSD-ESS2-2004. →
European Social Survey (2006). European social survey round 3 data. https://doi.org/10.21338/NSD-ESS3-2006. →
European Social Survey (2008). European social survey round 4 data. https://doi.org/10.21338/NSD-ESS4-2008. →
European Social Survey (2010). European social survey round 5 data. https://doi.org/10.21338/NSD-ESS5-2010. →
European Social Survey (2012). European social survey round 6 data. https://doi.org/10.21338/NSD-ESS6-2012. →
European Social Survey (2014). European social survey round 7 data. https://doi.org/10.21338/NSD-ESS7-2014. →
European Social Survey (2016). European social survey round 8 data. https://doi.org/10.21338/NSD-ESS8-2016. →
European Social Survey (2018). European social survey round 9 data. https://doi.org/10.21338/NSD-ESS9-2018. →
Felderer, B., Kirchner, A., & Kreuter, F. (2019). The effect of survey mode on data quality: disentangling nonresponse and measurement error bias. Journal of Official Statistics, 35(1), 93–115. https://doi.org/10.2478/jos-2019-0005. →
Gedeshi, I., Kritzinger, S., Poghosyan, G., Rotman, D., Pachulia, M., Fotev, G., Kolenović-Đapo, J., Rabušic, L., Baloban, J., Frederiksen, M., Saar, E., Ketola, K., Wolf, C., Pachulia, M., Bréchon, P., Voas, D., Rosta, G., Jónsdóttir, G. A., Rovati, G., et al. (2020). European Values Study 2017: integrated dataset (EVS 2017). Köln: GESIS. https://doi.org/10.4232/1.13511. →
Gedeshi, I., Zulehner, P. M., Rotman, D., Titarenko, L., Billiet, J., Dobbelaere, K., Kerkhofs, J., Swyngedouw, M., Voyé, L., Fotev, G., Marinov, M., Raichev, A., Stoychev, K., Kielty, J. F., Nevitte, N., Baloban, J., Roudometof, V., Rabusic, L., Rehak, J., et al. (2020). European Values Study longitudinal data file 1981–2008 (EVS 1981–2008). Köln: GESIS. https://doi.org/10.4232/1.13486. →
Goyder, J., & Leiper, J. M. (1985). The decline in survey response: a social values interpretation. Sociology, 19(1), 55–71. https://doi.org/10.1177/0038038585019001006 →
Greaves, L. M., Oldfield, L. D., Von Randow, M., Sibley, C. G., & Milne, B. J. (2020). How low can we go? Declining survey response rates to new zealand electoral roll mail surveys over three decades. Political Science, 72(3), 228–244. https://doi.org/10.1080/00323187.2021.1898995. →
Groves, R. M. (2006). Nonresponse rates and nonresponse bias in household surveys. Public Opinion Quarterly, 70(5, Special Issue), 646–675. https://doi.org/10.1093/poq/nfl033 →
Groves, R. M., & Cooper, M. (1998). Nonresponse in household interview surveys. Hoboken: Wiley. a, b
Groves, R. M., & Heeringa, S. G. (2006). Responsive design for household surveys: tools for actively controlling survey errors and costs. Journal of the Royal Statistical Society: Series A (Statistics in Society), 169(3), 439–457. https://doi.org/10.1111/j.1467-985x.2006.00423.x. →
Groves, R. M., & Peytcheva, E. (2008). The impact of nonresponse rates on nonresponse bias: a meta-analysis. Public Opinion Quarterly, 72(2), 167–189. https://doi.org/10.1093/poq/nfn011 →
Gummer, T. (2019). Assessing trends and decomposing change in nonresponse bias. Sociological Methods Research, 48(1), 92–115. https://doi.org/10.1177/0049124117701479. →
de Heer, W. (1999). International response trends: results of an international survey. Journal of Official Statistics, 15(2), 129–142. →
ISSP Research Group (2002). International Social Survey Programme: social inequality III-ISSP 1999. https://doi.org/10.4232/1.3430. →
ISSP Research Group (2003). International Social Survey Programme: environment II—ISSP 2000. https://doi.org/10.4232/1.3440. →
ISSP Research Group (2009). International Social Survey Programme: leisure time and sport-ISSP 2007. https://doi.org/10.4232/1.10079. →
ISSP Research Group (2012a). International Social Survey Programme: citizenship—ISSP 2004. https://doi.org/10.4232/1.11372. →
ISSP Research Group (2012b). International Social Survey Programme: national identity II—ISSP 2003. https://doi.org/10.4232/1.11449.
ISSP Research Group (2013a). International Social Survey Programme: family and changing gender roles III—ISSP 2002. https://doi.org/10.4232/1.11564. →
ISSP Research Group (2013b). International social survey programme: work orientations III—ISSP 2005. https://doi.org/10.4232/1.11648.
ISSP Research Group (2015a). International Social Survey Programme: health and health care-ISSP 2011. https://doi.org/10.4232/1.12252. →
ISSP Research Group (2015b). International Social Survey Programme: national identity III—ISSP 2013. https://doi.org/10.4232/1.12312.
ISSP Research Group (2016a). International Social Survey Programme: citizenship II—ISSP 2014. https://doi.org/10.4232/1.12590. →
ISSP Research Group (2016b). International Social Survey Programme: family and changing gender roles IV—ISSP 2012. https://doi.org/10.4232/1.12661.
ISSP Research Group (2017a). International Social Survey Programme: social inequality IV—ISSP 2009. https://doi.org/10.4232/1.12777. →
ISSP Research Group (2017b). International Social Survey Programme: work orientations IV—ISSP 2015. https://doi.org/10.4232/1.12848.
ISSP Research Group (2018a). International Social Survey Programme: religion III—ISSP 2008. https://doi.org/10.4232/1.13161. →
ISSP Research Group (2018b). International Social Survey Programme: role of government V—ISSP 2016. https://doi.org/10.4232/1.13052.
ISSP Research Group (2019a). International Social Survey Programme: environment III—ISSP 2010. https://doi.org/10.4232/1.13271. →
ISSP Research Group (2019b). nternational social survey programme: social networks and social resources—ISSP 2017
ISSP Research Group (2020). International Social Survey Programme: religion IV—ISSP 2018. https://doi.org/10.4232/1.13543. →
ISSP Research Group (2021). International Social Survey Programme: role of government IV-ISSP 2006. https://doi.org/10.4232/1.13707. →
Jabkowski, P. (2022). Sampling and fieldwork practices in europe (SaFPE). https://doi.org/10.17605/OSF.IO/2QPBD. →
Jabkowski, P., & Cichocki, P. (2019). Within-household selection of target-respondents impairs demographic representativeness of probabilistic samples: evidence from seven rounds of the European social survey. Survey Research Methods, 13(2), 167–180. https://doi.org/10.18148/srm/2019.v13i2.7383. a, b
Jabkowski, P., & Kołczyńska, M. (2020). Sampling and fieldwork practices in europe: analysis of methodological documentation from 1,537 surveys in five cross-national projects, 1981–2017. Methodology, 16(3), 186–207. https://doi.org/10.5964/meth.2795. a, b, c, d
Jabkowski, P., Cichocki, P., & Kołczyńska, M. (2023). Multiproject assessments of sample quality in crossnational surveys: the role of weights in applying external and internal measures of sample bias. Journal of Survey Statistics and Methodology 11(2). https://doi.org/10.1093/jssam/smab027. a, b, c, d
Kohler, U. (2007). Surveys from inside: an assessment of unit nonresponse bias with internal criteria. Survey Research Methods, 1, 55–67. https://doi.org/10.18148/SRM/2007.V1I2.75. a, b, c, d
Kohler, U., Sawert, T., & Class, F. (2024). Control variable selection in applied quantitative sociology: a critical review. European Sociological Review 40(1), 173–186. https://doi.org/10.1093/esr/jcac078. a, b
Kreuter, F. (2013). Facing the nonresponse challenge. The Annals of the American Academy of Political and Social Science, 645(1), 23–35. https://doi.org/10.1177/0002716212456815. →
Laurie, H., Smith, R., & Scott, L. (1999). Strategies for reducing nonresponse in a longitudinal panel survey. Journal of Official Statistics, 15(2), 269–282. →
Leeper, T. J. (2019). Where have all the respondents gone? Public Opinion Quarterly, 83(S1), 280–288. https://doi.org/10.1093/poq/nfz010. a, b
de Leeuw, E. D., & de Heer, W. (2002). Trends in household survey nonresponse: a longitudinal and international comparison. In R. M. Groves, A. D. Dillman, J. Eltinge & R. Little (Eds.), Survey nonresponse (pp. 41–54). Hoboken: Wiley. →
Lugtig, P., Lensvelt-Mulders, G. J., Frerichs, R., & Greven, A. (2011). Estimating nonresponse bias and mode effects in a mixed-mode survey. International Journal of Market Research, 53(5), 669–686. https://doi.org/10.2501/ijmr-53-5-669-686. →
Lundberg, I., Johnson, R., & Stewart, B. M. (2021). What is your estimand? Defining the target quantity connects statistical evidence to theory. American Sociological Review, 86(3), 532–565. https://doi.org/10.1177/00031224211004187. →
Lundquist, P., & Särndal, C.-E. (2013). Aspects of responsive design with applications to the Swedish Living Conditions Survey. Journal of Official Statistics, 29(4), 557–582. https://doi.org/10.2478/jos-2013-0040. →
Manfreda, K. L., Bosnjak, M., Berzelak, J., Haas, I., & Vehovar, V. (2008). Web surveys versus other survey modes: a meta-analysis comparing response rates. International Journal of Market Research, 50(1), 79–104. https://doi.org/10.1177/147078530805000107. →
Massey, D. S., & Tourangeau, R. (2012). Where do we go from here? Nonresponse and social measurement. The Annals of the American Academy of Political and Social Science, 645(1), 222–236. https://doi.org/10.1177/0002716212464191 →
Meng, X.-L. (2018). Statistical paradises and paradoxes in big data (I): law of large populations, big data paradox, and the 2016 US presidential election. The Annals of Applied Statistics, 12(2), 685–726. https://doi.org/10.1214/18-AOAS1161SF. →
Menold, N. (2014). The influence of sampling method and interviewers on sample realization in the European Social Survey. Survey Methodology, 40, 105–123. a, b
Ortmanns, V., & Schneider, S. L. (2016). Can we assess representativeness of cross-national surveys using the education variable? Survey Research Methods, 10(3), 189–210. https://doi.org/10.18148/srm/2016.v10i3.6608. →
Pearl, J. (1994). Causal diagrams for empirical research. Biometrika, 82(4), 669–710. →
Pearl, J. (2009). Causality: models, reasoning, and inference (2nd edn.). Cambridge: Cambridge University Press. →
Pearl, J., & Mackenzie, D. (2018). The book of why. The new science of cause and effect. New York: Basic Books. →
Pickery, J., & Loosveldt, G. (2002). A multilevel multinomial analysis of interviewer effects on various components of unit nonresponse. Quality&Quantity, 36(4), 427–437. https://doi.org/10.1023/A:1020905911108. →
Richter, G., Wolfram, T., & Weber, C. (n.d.). Die Statistische Methodik von Civey. Eine Einordnung im Kontext gegenwärtiger Debatten über das Für und Wider internetbasierter nicht-probabilistischer Stichprobenziehung. https://civey.com/whitepaper →
Roberts, C., Vandenplas, C., & Ernst Stähli, M. (2014). Evaluating the impact of response enhancement methods on the risk of nonresponse bias and survey costs. Survey Research Methods, 8(2), 67–80. https://doi.org/10.18148/srm/2014.v8i2.5459. →
Rogers, A., Murtaugh, M. A., Edwards, S., & Slattery, M. L. (2004). Contacting controls: are we working harder for similar response rates, and does it make a difference? American Journal of Epidemiology, 160(1), 85–90. https://doi.org/10.1093/aje/kwh17. →
Särndal, C.-E. (2011). The 2010 Morris Hansen Lecture: dealing with survey nonresponse in data collection, in estimation. Journal of Official Statistics, 27(1), 121. →
Schnell, R. (1997). Nonresponse in Bevölkerungsumfragen Ausmass, Entwicklung und Ursachen. Wiesbaden: VS. →
Schnell, R., & Kreuter, F. (2000). Untersuchungen zur Ursache unterschiedlicher Ergebnisse sehr ähnlicher Viktimisierungssurveys. Kölner Zeitschrift für Soziologie und Sozialpsychologie, 1, 96–117. →
Schouten, B., Cobben, F., & Bethlehem, J. (2009). Indicators for the representativeness of survey response. Survey Methodology, 35(1), 101–113. https://www150.statcan.gc.ca/n1/pub/12-001-x/2009001/article/10887-eng.pdf a, b
Schouten, B., Shlomo, N., & Skinner, C. (2011). Indicators for monitoring and improving representativeness of response. Journal of Official Statistics, 27(2), 231253. a, b
Singer, E. (2006). Introduction: Nonresponse bias in household surveys. Public Opinion Quarterly, 70(5), 637–645. https://doi.org/10.1093/poq/nfl034. →
Sodeur, W. (1997). Interne Kriterien zur Beurteilung von Wahrscheinlichkeitsauswahlen. ZA-Information, 41, 58–82. a, b, c
Sodeur, W. (2007). Entscheidungsspielräume von Interviewern bei der Wahrscheinlichkeitsauswahl. Methoden, Daten, Analysen, 1(2), 107–130. →
Stedman, R. C., Connelly, N. A., Heberlein, T. A., Decker, D. J., & Allred, S. B. (2019). The end of the (research) world as we know it? Understanding and coping with declining response rates to mail surveys. Society Natural Resources, 32(10), 1139–1154. https://doi.org/10.1080/08941920.2019.1587127. →
Steeh, C. G. (1981). Trends in nonresponse rates, 1952-1979. Public Opinion Quarterly, 45(1), 40–57. https://doi.org/10.1086/268633 →
Steeh, C. G., Kirgis, N., Cannon, B., & DeWitt, J. (2001). Are they really as bad as they seem? Nonresponse rates at the end of the twentieth century. Journal of Official Statistics, 17(2), 227–247. →
Struminskaya, B., Kaczmirek, L., Schaurer, I., & Bandilla, W. (2014). Assessing representativeness of a probability-based online panel in Germany. In Online panel research: A data quality perspective (pp. 61–85). Chichester: John Wiley & Sons, Ltd. https://doi.org/10.1002/9781118763520.ch3. →
Tourangeau, R. (2017). Mixing modes: tradeoffs among coverage, nonresponse, and measurement error. In P. P. Biemer, E. de Leeuw, S. Eckman, B. Edwards, F. Kreuter, L. E. Lyberg, N. C. Tucker & B. T. West (Eds.), Total survey error in practice. Hoboken: Wiley. →
Tourangeau, R., & Plewes, T. J. (Eds.). (2013). Nonresponse in social science surveys: a research agenda. Washington, DC: National Academies Press. →
Vehovar, V. (1999). Field substitution and unit nonresponse. Journal of Official Statistics, 15(2), 335–350. →
Yeager, D. S., Krosnick, J. A., Chang, L., Javitz, H. S., Levendusky, M. S., Simpser, A., & Wang, R. (2011). Comparing the accuracy of RDD telephone surveys and internet surveys conducted with probability and non-probability samples. Public Opinion Quarterly, 75(4), 709–747. https://doi.org/10.1093/poq/nfr020. a, b