This article (https://doi.org/10.18148/srm/2024.v18i3.8309) contains supplementary material.
For the estimation of a relative size π of a subgroup A of a study population U with size N (A ⊆ U), let variable y indicate the membership or non-membership of this group for a population unit k (k ∈ U):
Hence, the parameter π is given by
(ΣU denotes the sum over all N population units). In a general probability sample s of size n drawn without replacement, the design-unbiased Horvitz-Thompson-based estimator of π is given by
(Σs denotes the sum over all n sample units). Therein, dk denotes the design weight of unit k, defined as usual as the reciprocal of the first-order sample inclusion probability ωk of sample unit k (cf., for instance, Särndal et al., 1992, p. 43 ff).
When questions on sensitive topics, such as tax morality, academic cheating, domestic violence, harassment at work, cyber mobbing, illegal work, sexual behavior, or racism, to name only a few examples, are directly asked in statistical surveys, the rates of nonresponse as well as untruthful answering might increase above the usual levels and the drawn sample s be decomposed into three disjoint parts: one part consisting of the sample units who respond truthfully; a second one consisting of the units who respond untruthfully; and a third one consisting of the units for which y cannot be observed at all. This imposes measurement and nonresponse errors on the estimation. Consequently, the estimator πHT based only on the response set, consisting only of the first two of these parts of the sample s may be strongly biased (cf., for instance, Tourangeau & Yan, 2007, p. 862 f). Before having to apply the statistical methods of weighting adjustment and data imputation to try at least to compensate for the occurred nonresponse, but not for the untrue answers hidden in the response set, data collectors should do everything to keep both rates, that of non-responses and that of untrue answers, as low as possible.
Indirect questioning (IQ) designs such as the “randomized response (RR) methods,” the “item count technique” (“unmatched count technique” or “list experiment”), or the “nonrandomized response (NRR) models” aim precisely at addressing both problems, untruthful and missing answers, before they occur. The common characteristic of all IQ designs is that they “mask” the true status of a survey participant with respect to the sensitive study variable y, so that an experimenter is not able to conclude from the given process answer directly to this variable. This privacy-protecting effect shall ensure the respondents’ cooperation (for an overview of IQ designs, see Chaudhuri & Christofides, 2013, or Chaudhuri et al., 2016).
However, to be seen as a serious competitor to the direct questioning-practice common in empirical research, IQ designs have to be simple to implement in several survey modes for the experimenters and easy to understand for the respondents. Moreover, their theory must be as general as possible to be applicable with all probability sampling schemes because in fields, in which sensitive questions are asked, more often than not complex sampling schemes with unequal inclusion probabilities including stratification and/or clustering are used.
The pioneering work in this field was published by Warner (1965). In his RR technique (for an introduction see, for example, Genest et al., 2024), one of the following two statements S1 and S2 is randomly assigned to a survey participant with unequal probabilities:
S1: I am a member of group A (for example: I cheated on an exam last semester).
S2: I am a member of group AC (for example: I did not cheat on an exam last semester).
(AC = U − A). If the randomly selected statement applies to the respondent, she or he has to provide a “yes”-process answer, otherwise a “no.” This questioning design does not enable the experimenter to link the given process answer of respondent k with certainty to the true value yk.
Since this initial boost, various other RR methods have been developed. All of these questioning designs require a randomization instruction to select the statement that the respondent has to answer. This instruction can be employed either explicitly by the usage of a randomization device such as dice, a spinner, or a digital random number generator (cf., for instance, Peeters et al., 2010), or implicitly by a preceding randomizing question on the membership of a certain population subset R ⊆ U, unrelated to the sensitive subject and of known relative size. In such a case, to ensure the respondent’s willingness to cooperate, the experimenter must, without any doubt, not know or be able to tell the respondent’s answer to such a question. Therefore, a question on the birth date, age, phone or house number of a person determined by the experimenter (e.g., the interviewee herself or himself, her or his mother or father), although this is often suggested in the literature, is conceivably unsuitable. Instead, it is advisable to let the respondent choose the reference person herself or himself beforehand, which mimics the usage of a randomization device (see Quatember, 2019, p. 271). For this purpose, the implicit randomization instruction could be formulated in the following way: ‘Think of a person (you, your mother, a friend, someone else) whose date of birth you know but without revealing this information and stick to it. If the birth date lies within the interval from January to September, then answer on the first statement, otherwise the second.’
Two obvious weaknesses of the RR techniques are: a) If a randomization device is used, the practical applicability is limited; b) the RR procedure may nevertheless end up with the sensitive question, the sensitivity of which was precisely the starting point of the considerations.
To overcome these weaknesses, Yu et al. (2008) introduced the NRR models (see also Tan et al., 2009, or Tian & Tang, 2014). These questioning designs can be seen as device-free transformations of RR models, in which the interviewees never have to supply the answer to the sensitive question directly. Instead, the process answer “yes” or “no” that has to be provided by a respondent is a function of the number of the applicable of two different statements. The positive effect of these design features on the comprehensibility of the questioning design and the perceived privacy protection in comparison to RR questioning designs was shown in several experimental studies (cf., for instance, Höglinger et al., 2016; Hoffmann et al., 2017). Furthermore, in so-called “strong validation studies” with known prevalence of various control attributes, NRR methods have been shown to work in the intended direction (cf., for instance, Hoffmann et al., 2015; Hoffmann & Musch, 2016). Nevertheless, it shall not be concealed that there are also critical voices who have not found such positive effects of these designs in their respective experimental set-ups (see the related discussion in Sect. 5 below).
In the next section of this methodological article, the already published NRR survey designs are discussed along with their practical implementations in the questionnaires that can be applied even in self-administered surveys. In Sect. 3, NRR versions of two well-established practically used RR techniques, the forced RR model and the contamination method, are presented. In the fourth section, for all NRR designs, the theory for the estimation of a population proportion is developed for general probability sampling under a unified theoretical roof. In addition, in that section, these NRR questioning designs are compared in terms of their inherent privacy protection. Sect. 5 also acknowledges the non-statistical aspects that influence the data quality in surveys on sensitive topics when NRR models are applied. Eventually, a “Summary and Conclusions”-section concludes the article.
The “crosswise (=) model” introduced by Yu et al. (2008) is a transformation of Warner’s RR technique with implicit randomization instruction (see Sect. 1) into an NRR questioning design. The randomization instruction refers to a respondent k’s membership of group R ⊆ U, unrelated to the membership of group A, with membership indicator
and given probability P(rk = 1) = (0 < < 1).
The NRR version of this RR technique can be implemented into a questionnaire in the following manner (here and in the following, the abstract formulations on membership of certain groups will be used):
Look at the following two statements:
S1: I am a member of group A (yk = 1).
S2: I am a member of group R (rk = 1).
If none or both of these two statements apply to you, please answer “yes” (), otherwise answer “no” ().
In contrast to the original RR technique, in the model, the interviewee is not faced with a single randomly selected statement but shall answer “yes” or “no,” respectively, depending on the number of the applicable of two statements. This questioning design was called “crosswise model” because when the four possible combinations of y and r are presented in a 2-dimensional table (see Table 1), those combinations of y and r, resulting in the same of the two possible process answers
of respondent k, can be connected by two imaginary lines that “cross” each other. In the original publication, respondents were asked to “truthfully put a tick in the main diagonal or in the antidiagonal” of such a table implemented in the questionnaire (Yu et al., 2008, p. 255).
Table 1 The crosswise model by Yu et al. (2008) with the corresponding marginal probabilities of variables y and r
y\r | rk = 0 (1 − ) | rk = 1 () |
yk = 0 (1 − π) | ||
yk = 1 (π) |
The crosswise model is a formal equivalent of Warner’s RR technique with a design probability for the selection of statement S1. For a given status of the variable y under study, the probability of is given by
and the term
with ≡ 2 · − 1 ( ≠ 0) and ≡ 1 − is an ‑unbiased estimator for the true status yk of respondent k with respect to the sensitive variable y in the sense that . For → 1 (or → 0, respectively), the model converges against the direct questioning on the membership of group A (or AC).
The model was applied, for example, in surveys on different topics such as the use of anabolic steroids, xenophobia, prejudices against women leaders, tax evasion, or voting preference (cf., for instance, Nakhaee et al., 2013; Kundt et al., 2017; Waubert de Puiseau et al., 2017; or the various examples listed in Schnell & Thomas 2023).
The other NRR questioning design published in the initial article by Yu et al. (2008) was called the “triangular (=) model.” It is an NRR version of an RR method, which was introduced in different forms by Horvitz et al. (1976), Mangat (1994), and Clark & Desharnais (1998). In this method, each respondent has either to answer truthfully the sensitive question with the given design probability or is instructed to answer “yes” regardless of its membership status with respect to group A with the remaining probability (0 < < 1). For its NRR version, the same table is used as for the ‑model. But in this case, also the combination (yk = 1, rk = 0) results in the process answer “yes” (see Table 2).
Table 2 The triangular model by Yu et al. (2008) with the corresponding marginal probabilities of variables y and r
y\r | rk = 0 (1 − ) | rk = 1 () |
yk = 0 (1 − π) | ||
yk = 1 (π) |
For the practical implementation of the model into questionnaires, one may proceed as follows:
Look at the following two statements:
S1: I am a member of group A (yk = 1).
S2: I am a member of group RC (rk = 0).
If at least one of the two statements applies to you, please answer “yes” (), otherwise answer “no” ().
The term “triangular model” refers to the fact that in a 2-dimensional presentation of this NRR questioning design, those combinations of y and r, resulting in the process answer “yes” of a respondent k (), are now on the corner points of a triangle.
In the model, the probability of is given by
Therefore, the term
with α ≡ (α ≠ 0) and ≡ 1 − is ‑unbiased for yk in the sense that . For → 1, the model converges against the direct questioning on the membership of group A.
The model was applied, for example, by Moshagen et al. (2012) in a survey on domestic violence, by Frenger et al. (2016) in a study on substance use of amateur athletes, and by Hoffmann et al. (2020) in an empirical comparison study with the model on xenophobia. Perri et al. (2022) reported on studies on racism and workplace bullying using the as well as the model.
The (steep) “parallel (=) model”, introduced by Tian (2014), is an NRR version of the unrelated question RR design (Horvitz et al., 1967, and Greenberg et al., 1969). With the aim to further increase the respondents’ perceived privacy protection, this specific RR approach complements the first statement of Warner’s RR method with a second statement on the non-sensitive membership of a certain population subset B ⊆ U unrelated to the sensitive subject.
In the NRR version of this RR method with known population prevalence πB of the membership of group B (0 < πB < 1), a respondent k is faced with two different pairwise combinations of items in the two statements. The first statement refers to variables r from the randomization instruction of Sect. 2.1 (with P(rk = 1) = and 0 < < 1), and y from the model. The second statement refers to variables r and x, the latter indicating the membership of the non-sensitive group B of the unrelated question model:
The model can be implemented into the questionnaire in the following way:
Look at the following two statements:
S1: I am a member of group A and also of group R (yk = 1, rk = 1).
S2: I am a member of group B and also of group RC (xk = 1, rk = 0).
If one of these statements applies to you, please answer “yes” (), otherwise answer “no” ().
Note: To avoid using a statement with two variables included, here and in the following sections one can alternatively formulate statement S1 as below by defining two items I and J beforehand (S2 likewise):
I: I am a member of group A (yk = 1).
J: I am a member of group R (rk = 1).
S1: Both items I and J apply to me (yk = 1, rk = 1).
The name “parallel model” of this specific NRR questioning design is again deduced from its representation in a 2-dimensional table, in which the pairwise combinations resulting in the same of the two possible process answers of a respondent k can be connected by two parallel lines (see Table 3). We rename this model the “steep parallel model” to distinguish it from the “flat parallel model” which will be presented in Sect. 3.2.
Table 3 The steep parallel model by Tian (2014) with the corresponding marginal probabilities of variables y, x, and r
x, y\r | rk = 0 (1 − ) | rk = 1 () |
xk = 0 (1 − πB) | – | |
xk = 1 (πB) | – | |
yk = 0 (1 − π) | – | |
yk = 1 (π) | – |
For the model, the probability of a “yes”-response () is given by
Consequently, the term
with ≡ ( ≠ 0) and ≡ (1 − ) · πB is ‑unbiased for yk with . For πB → 1, the model converges against the model with = . For → 1, the model converges against the direct questioning on the membership of group A.
The original unrelated RR technique was applied, for example, in studies on induced abortion (Abernathy et al., 1970) or in case studies on premarital sex and plagiarism among students (Tian, 2014).
In the next section, two new NRR models will be proposed, which are transformations of well-established and practically applied RR questioning designs, namely of the “forced RR method” and the “contamination method,” in order to make also these RR methods applicable to all types of survey modes without the need of a randomization device. Practitioners who have made good experiences with one of these two RR techniques may wish to use their NRR-version, which is simpler to implement and easier for the respondents to understand.
The forced RR method is very popular among applied researchers. This is documented by a large variety of application examples with studies on xenophobia and anti-Semitism, poaching among farmers, doping of fitness studio users, or criminal acts among prison populations (cf., for instance, Krumpal, 2012; St John et al., 2012; Cobo et al., 2021). For this method, the needed implicit randomization instruction divides the population into three disjoint groups Q1, Q2, and Q3 according to the three categories of a variable q, which is unrelated to y: group Q1 with a population prevalence of , group Q2 with one of , and group Q3 with one of 1 − − (; i = 1, 2, 3; ). These different groups could, for instance, be built by three disjoint intervals of possible birth dates. The membership of respondent k with respect to one of these groups is indicated by
The RR method, which will subsequently be transformed into the “double triangular (=) NRR model,” can be described in the following way (Boruch, 1971; Fidler & Kleinknecht, 1977; Fox & Tracy, 1986): Each respondent has either to answer the sensitive statement with probability , is instructed to say “yes” with probability or “no” with the remaining probability 1 − − , both regardless of the membership of A or AC.
In the questionnaire, the model may be implemented in the following way:
Look at the following two statements:
S1: I am a member of group A and also of group Q2 (yk = 1, qk = 2).
S2: I am a member of group Q1 (qk = 1).
If one of these statements applies to you, please answer “yes” (), otherwise answer “no” ().
In consistency with the representations of the NRR models in Table 1, 2 and 3 from Sect. 2, this NRR design is named the “double triangular model” because those combinations of variables y and q that result in the same of the two possible process answers z can be connected by two triangles (Table 4).
Table 4 The double triangular model with the corresponding marginal probabilities of variables y and q
y\q | qk = 1 () | qk = 2 () | qk = 3 (1 − − ) |
Yk = 0 (1 − π) | |||
Yk = 1 (π) |
For this questioning design, the probability of a “yes”-answer () is given by
Therefore, in this case, the term
with ( ≠ 0) and is ‑unbiased for yk in the sense that . For , the model converges against the model with = . For → 1, the model converges against the direct questioning on the membership of group A.
The “contamination RR method” was introduced by Boruch (1972) and will now be transformed into the “flat parallel (= ) NRR model.” Kuk (1990) and Christofides (2009) presented this RR technique in the following way: The memberships of two certain population subgroups R ⊆ U and V ⊆ U, defined beforehand, are unrelated to the membership of A. For respondent k, as in the model, the membership indicator with respect to R (from Sect. 2.1) is given by rk with P(rk = 1) = (0 < < 1) and the membership indicator with respect to V is given by
with P(vk = 1) = (0 < < 1) and . If the respondent k is a member of group A, she or he has to answer “yes” only if k ∈ R, otherwise “no”, regardless of the membership/non-membership of group V. If the respondent is a member of group AC, the process response is “yes” only if k ∈ V, and otherwise “no”, regardless of the membership/non-membership of group R.
When it comes to the sensitive topic in the questionnaire, the NRR version of the contamination method can be implemented in the following way:
Look at the following two statements:
S1: I am a member of group A and also of group R (yk = 1, rk = 1).
S2: I am a member of group AC and also of group V (yk = 0, vk = 1).
If one of these statements applies to you, please answer “yes” (), otherwise answer “no” ().
When compared to the steep parallel model by Tian (2014) from Sect. 2.3, the representation of this NRR design in a 2-dimensional table can be called the “flat parallel model” (Table 5) because in such a table, those two combinations that lead to the same process answer or , respectively can be connected by one of two possible flat parallel lines.
Table 5 The flat parallel model with the corresponding marginal probabilities of variables y, r, and v
y\r | rk = 0 (1 − ) | rk = 1 () | vk = 0 (1 − ) | vk = 1 () |
yk = 0 (1 − π) | – | – | ||
yk = 1 (π) | – | – |
The probability of a process-answer “yes” () is given by
Therefore, the term
with ( ≠ 0) and is ‑unbiased for yk with .
For and , the model converges against the model with . Moreover, for , the model converges against the model with = . Eventually, for → 1 and → 0, the model converges against the direct questioning on the membership of group A.
In the direct questioning approach, under the assumption of full cooperation of the selected sample units, the theoretical variance of the design-unbiased estimator
from Eq. 2 is given by
with ∆kl = ωkl − ωk · ωl, the covariance of the sample inclusion indicators Ik and Il, where Ik = 1 if a population element k is included in the sample and zero otherwise (k, l ∈ U). In ∆kl, ωkl denotes the second-order sample inclusion probability that elements k and l of U are both in s. For the variance ∆kk of these indicators, ∆kk = ωk · (1 − ωk) applies (cf., for instance, Särndal et al., 1992, p. 36). Provided that ωkl > 0 for k, l ∈ U, a design-unbiased estimator of V(πHT) is calculated by
(cf., for instance, Särndal et al., 1992, p. 43 ff).
In the following, under the assumption of full cooperation the estimators for π are developed along with their variances and variance estimators for all five NRR questioning designs from Sects. 2 and 3 ( = , , , , ) for general probability sampling under one theoretical roof: In the unified model, the probability of a process answer “yes” () is given by
(see Sects. 2 and 3). Therefore, the term
(α ≠ 0) is ‑unbiased for yk () and in the NRR model ,
is ‑unbiased for π from Eq. 1. For the specific values of α and β in (10) and (11) for the five different NRR designs, see the terms from Eqs. 3–7 in Sects. 2 and 3. Note that π could be outside the interval [0;1]. For such cases, the maximum-likelihood estimator using the EM algorithm is a possible solution (Quatember, 2014; Tian et al., 2017). If non-ignorable nonresponse still occurs, for the application of weighting adjustment techniques see Barabesi et al. (2014).
The theoretical variance of π is given by
Therein, γ and δ are defined as the following functions of α and β : , . For the specific values of γ and δ in the respective NRR design, see Table 6. The first component of the sum on the right-hand side of the variance (13) of π refers to the variance (8) of the estimator πHT in the direct questioning approach under the assumption of full cooperation. Hence, the second component can be seen as the additional cost in terms of variance for the intended bias reduction when compared to the direct questioning with its nonresponse and untruthful answers.
Table 6 Terms for γ and δ, from Eq. 13 and and from Eqs. 18 and 19 for the NRR designs = , , , , and
NRR design | γ | δ | ||
0 | ||||
1 − | 0 | |||
The variance from Eq. 13 can be unbiasedly estimated by
For the proofs of Eqs. 13 and 14, see Appendix 1.
Inserting, for example, the design weights dk = N/n for all sample units k ∈ s for simple random without replacement (SI) sampling in formulas (12) to (14) results in the easy-to-handle terms for the SI sampling scheme: The estimator for π is given by
with the simple sample mean
of all responses in the SI sample s. The theoretical variance of yields
which is unbiasedly estimated by
For the proofs of Eqs. 16 and 17, see Appendix 2.
NRR questioning designs aim to protect the respondents’ privacy strongly enough that they are willing to truthfully participate in a survey, even if the topic is of a delicate kind. For the comparison of the respective privacy protection levels, a measure of the level of privacy protection with respect to a process answer “yes” () of a respondent k can be calculated by
The measure is the ratio of the minimum and the maximum of the probability of the process response “yes” () from Eq. 10, given the respondent k is a member of group A () or a non-member (). For α > 0, Eq. 18 results in , whereas for α < 0, which is possible, though unusual, in both the model and the model, it results in . Regarding a “no”-answer (), this measure is given by
(Quatember, 2019). For α > 0, Eq. 19 results in , whereas for α < 0, applies.
These privacy protection measures range from 0 to 1. They equal to zero only if a “yes”- (or a “no”-) process answer would directly reveal the membership of group A or AC like in the direct questioning approach. The more these measures differ from zero, the more is the respondent’s privacy protected against the experimenter. The maximum value of one would mean a totally protected privacy so that the given response does not contain information about the true value yk of the unit anymore. The two levels of privacy protection offered by the NRR model are completely under the control of the experimenter (because they depend solely on the chosen design probabilities) and can be found in the last two columns of Table 6.
For the crosswise model , for instance, the values of these measures depend solely on the design probability . Looking at Table 6, it can be seen that the model is the only questioning design among the five presented models, for which the two possible process answers and are always equally protected (). Such a balanced survey design does not offer any self-protective answer option because none of the two possible answers is likely to arouse the respondent’s fear that the response might be directly associated with the true status of variable y under study by the experimenter. Consequently, not answering at all could be seen as an admission of the sensitive behavior rather than a truthful answer in the model (Kundt et al., 2017, p. 116).
In contrast to the model, the triangular model is maximally unbalanced with respect to privacy protection because the process response “no” fully reveals the respondent’s non-membership of group A (, ). This maximum asymmetry of the process answers could be perceived as unproblematic if only the membership of group A but not of AC was sensitive. However, it provides respondents with a perfectly safe response strategy to avoid the risk of being suspected as a member of group A. That strategy is to simply ignore the instructions and give the process answer “no.”
For the and the model, the two levels of privacy protection with respect to “yes”- and “no”-answers can be different but both are larger than zero (, i = 1,0). This offers experienced researchers the possibility to assign different levels of privacy protection to the possible process responses by an adequate choice of the design parameters (Quatember, 2009). Assuming there is no change in respondent cooperation, such a reduction of at least one of the privacy protection levels decreases the variance of the estimator compared to the model. From Eqs. 18 and 19, the parameters α and β can be expressed as functions of and (see Appendix 3). Inserting these expressions into the parameters γ and δ of the second component of variance expression (13) shows for all probability sampling schemes that the additional variance caused by the NRR questioning design depends solely on the privacy protection offered by the respective model. Questioning designs with design probabilities that yield the same privacy protection levels are always equally accurate in terms of variance, whereas designs with smaller levels are more accurate than designs with larger ones (cf., for instance, Guerriero & Sandri, 2007, Quatember, 2012, or Giordano & Perri, 2012). However, in the as well as the model, respondents might perceive a “no”-process answer as “safer” strategy if they fear that a “yes” could be interpreted as agreement to statement S1 (see Sects. 2.3 and 3.1). A non-compliance with the design instructions could be the consequence (for experiments on this aspect, see Edgell et al., 1982, or Coutts & Jann, 2011).
In fact, only the model is able to combine the advantages of the model as well as the and the model. On the one hand, like the model, the model offers absolutely no self-protective strategy because the membership of group A or group AC, respectively, is included in both statements of the method (see Sect. 3.2). On the other hand, like in the and also in the model, the privacy with respect to the two possible process responses and , respectively, can be protected differently if so desired to gain a positive effect on the estimation accuracy (, , i = 1,0). Eventually if both responses are to be protected equally, for , the model converges against the balanced model with = . This flexibility of the model can thus pay off in terms of both, cooperation willingness and accuracy.
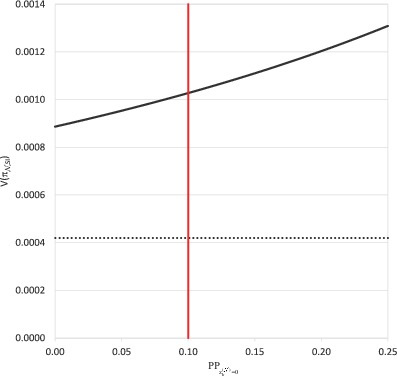
In the following, the variances of these different NRR designs are numerically compared to provide an impression of the effect of the proposed strategies on the accuracy of the estimation. For this purpose, we assume SI sampling with n = 500, π = 0.3, and . This specific level of privacy protection for a “yes”-response corresponds to the results derived from experiments on the cooperation-optimal choice of this measure for different sensitive variables by Fidler & Kleinknecht (1977) and Soeken & Macready (1982). Without loss of generality let us assume subsequently that applies. In Fig. 1, with these parameter values, the solid curve represents from Eq. 16 as a function of on the x‑axis, the level of privacy protection regarding a “no”-response. The dotted line shows the amount of the first component of Eq. 16. One can see that the model, for which only can apply, has the highest variance of 0.001309, whereas the model, for which only can apply, has the lowest of 0.000887. The variances of the , the , and the models, for which can apply, lie between these two extremes. If, for example, an experienced researcher determines that for a specific sensitive question a “no”-process answer has to be protected, but not to the same extent as a “yes”-answer, might be an appropriate choice (red line in Fig. 1). In this case, the application of the model with would overprotect the “no”-response. This would come at the cost of a loss of accuracy. However, the model with would not be applicable at all. The variances of the other three NRR models, for which could actually be set equal to 0.1, result in 0.001027. Compared to the model, this is a reduction of the second variance component of Eq. 16 by 32%.
As already mentioned in Sect. 1, besides the studies confirming the positive effect of the considered questioning designs on data quality in surveys on sensitive topics, there are also critical voices. For example, experiments by Höglinger & Diekmann (2017), Walzenbach & Hinz (2019), or Wolter & Diekmann (2021) showed that NRR questioning designs may also generate so-called “false positives,” meaning that respondents who actually do not belong to the sensitive group A of the target population provide a process response as if they did belong to this group. Therein, the occurrence of such false responses was empirically demonstrated to result mainly from problems concerning the use of certain non-sensitive randomizing questions and/or non-compliance with the design instructions (cf. also: Krause & Wahl, 2022, p. 48).
The first of these two aspects refers to the use of a randomizing question, for which the applied design probabilities (for example, and 1 − in the model) are not the correct ones, or which raises mistrust with regard to the promised privacy protection. The design probabilities must of course be known for the actual population under study to avoid a systematic bias of the estimator (see Online-Appendix C of Höglinger & Diekmann, 2017). Otherwise they would also have to be estimated in the sample survey (as suggested by Jerke et al., 2022, for example), which would further increase the imprecision of the sample results. Furthermore, pretests in expert discussions and cognitive interviews for the study by Jerke et al. (2022) on academic misconduct indicated that the commonly used non-sensitive questions such as on the respondent’s own birthday or house number or on the father’s or mother’s birthday raised mistrust among the respondents with respect to the promised privacy protection (p. 71). This could lead to deliberate non-compliance with the procedural instructions or random answers (Walzenbach & Hinz, 2023). Such a respondent’s behavior can also be caused by not understanding the question format. Therefore, data quality could be increased by providing understandable instructions combined with comprehension checks (examples of such instructions and comprehension questions can be found in Jann et al., 2012, Kundt et al., 2017, or Hoffmann et al., 2017, p. 1477). Meisters et al. (2020a) as well as Schnell & Thomas (2023) reported that this strategy was successfully applied at least to higher-educated populations.
Additionally, modified methodological approaches by Heck et al. (2018) and Meisters et al. (2022) enable to detect a certain type of deliberate non-adherence, the systematic preference for the answer option that is subjectively perceived as “safer” by the respondents. Careless cooperation on the part of respondents can also be the result of a low motivation to participate, as is generally observed in self-conducted (online) surveys, for example (cf., for example, Meisters et al., 2020a, p. 13). Empirical social researchers have been thinking about features, which positively affect the cooperation willingness of respondents in surveys. Dillman (2000) and Groves et al. (2004), for example, list several strategies to overcome a respondent’s “negative communicative intent” (Groves et al., 2004, p. 189 ff), all of which are certainly also applicable to indirect questioning designs. In addition, Schnapp (2019) suggested a method to adjust the model for the prevalence of random responding on the basis of follow-up questions.
The results of all these studies emphasize that a valid assessment of a questioning design must, as always, take into account various aspects, including its theoretical statistical properties, but also its impact on perceived privacy protection, its complexity in terms of respondents’ understanding, its practical applicability in statistical surveys, the survey mode, and all the other features that influence data quality. The identifiability of some of these aspects “in principle gives hope, because if these issues and the emergence of false positives are remedied, CM [the model] may be able to work as intended” (Wolter & Diekmann, 2021, p. 855). To assess the impact of untrue answers, Perri et al. (2022), for example, proposed a method for estimating the prevalence of liars. They included a direct question on the sensitive topic in an IQ design which allowed the experimenter to check whether the design was worth applying. Furthermore, Meisters et al. (2020b) suggested to induce a sensitive attribute with known prevalence to be able to conclude of the results whether or not false responses may have biased the results of the applied NRR approach.
In statistical surveys, sensitive topics lead to increased nonresponse and untruthful answering rates. Indirect questioning designs such as the randomized response methods, the item count technique, and the nonrandomized response models aim to reduce these rates by an inherent privacy protection that shall affect the respondents’ willingness to cooperate. However, in order to be seen as a serious competitor to the traditional direct questioning approach, such designs have to be simple to implement for the experimenters, easy to understand for the respondents and applicable to all probability sampling schemes. The randomized response techniques have several limitations in this respect. To overcome these limitations, nonrandomized response versions of these techniques have been developed, which are easier to understand for the respondents than their original randomized response versions.
In this methodological article, for the already existing NRR techniques, the crosswise model, the triangular model and the (steep) parallel model, easily applicable implementations in the questionnaires were presented. Two new NRR models, the double triangular model and the flat parallel model, were proposed, which are NRR versions of two well-established RR models, the forced RR method and the contamination technique. For all five NRR models, the theory for their application with general probability sampling is developed under one theoretical roof. Moreover, the respective privacy protection of these questioning designs is compared. Recommendations for the application of the different methods are derived from these considerations. The most flexible NRR technique, the flat parallel model, combines the advantage of the crosswise model, which does not offer self-protective answer options that can negatively affect the survey results, with the advantages of the steep parallel and the double triangular models. The latter models offer the possibility of assigning different levels of privacy protection to the “yes”- and “no”-responses with a positive effect on the estimation accuracy under the assumption of constant willingness to cooperate. As a consequence, this flexibility of the flat parallel model can pay off in terms of cooperation willingness as well as accuracy.
The proposed techniques should now be empirically compared with other IQ techniques as well as the direct questioning approach to determine how well they are able to mitigate both non-response and response bias and how susceptible they are to the problem of false positives.
I would like to thank the Editor and three learned reviewers for their very valuable comments and suggestions, which greatly contributed to the improvement of the article.
Abernathy, J. R., Greenberg, B. G., & Horvitz, D. G. (1970). Estimates of induced abortion in urban North Carolina. Demography, 7(1), 19–29. →
Barabesi, L., Diana, G., & Perri, P. F. (2014). Horvitz-Thompson estimation with randomized response and nonresponse. Model Assisted Statistics and Applications, 9, 3–10. https://doi.org/10.3233/MAS-130274. →
Boruch, R. F. (1971). Assuring confidentiality of responses in social research: a note on strategies. The American Sociologist, 6, 308–211. →
Boruch, R. F. (1972). Relations among statistical methods for assuring confidentiality of social research data. Social Science Research, 1, 403–414. https://www.sciencedirect.com/science/article/abs/pii/0049089X72900853?via%3Dihub. →
Chaudhuri, A., & Christofides, T. C. (2013). Indirect questioning in sample surveys. Heidelberg: Springer. →
Chaudhuri, A., Christofides, T. C., & Rao, C. R. (Eds.). (2016). Data gathering, analysis and protection of privacy through randomized response techniques: qualitative and quantitative human traits”. Handbook of statistics, Vol. 34. Amsterdam: Elsevier. →
Christofides, T. C. (2009). Randomized response without a randomization device. Advances and Applications in Statistics, 11(1), 15–28. →
Clark, S. J., & Desharnais, R. A. (1998). Honest answers to embarrassing questions: detecting cheating in the randomized response model”. Psychological Methods, 3(2), 160–168. https://doi.org/10.1037/1082-989X.3.2.160. →
Cobo, B., Castillo, E., López-Torrecillas, F., & Rueda, M. (2021). Indirect questioning methods for sensitive survey questions: modelling criminal behaviours among a prison population. PLoS ONE, 16(1), e245550. https://doi.org/10.1371/journal.pone.0245550. →
Coutts, E., & Jann, B. (2011). Sensitive questions in online surveys: Experimental results for the randomized response technique (RRT) and the unmatched count technique (UCT). Sociological Methods & Research, 40(1), 169–193. https://doi.org/10.1177/0049124110390768. →
Dillman, D. A. (2000). Mail and internet surveys (2nd edn.). New York: John Wiley & Sons. →
Edgell, S. E., Himmelfarb, S., & Duchan, K. L. (1982). Validity of forced responses in a randomized response model. Sociological Methods & Research, 11(1), 89–100. https://doi.org/10.1177/0049124182011001005. →
Fidler, D. S., & Kleinknecht, R. E. (1977). Randomized response versus direct questioning: two data collection methods for sensitive information. Psychological Bulletin, 84(5), 1045–1049. https://doi.org/10.1037/0033-2909.84.5.1045. a, b
Fox, J. A., & Tracy, P. E. (1986). Randomized response—a method for sensitive surveys. Beverly Hills: Sage University Papers. →
Frenger, M., Pitsch, W., & Emrich, E. (2016). Sport-induced substance use—an empirical study to the extent within a German sports association. PLoS ONE, 11(10), e165103. https://doi.org/10.1371/journal.pone.0165103. →
Genest, C., Hanley, J. A., & Bhatnagar, S. R. (2024). Investigating sensitive issues in class through randomized response polling. Journal of Statistics and Data Science Education. https://doi.org/10.1080/26939169.2024.2302179. →
Giordano, S., & Perri, P. F. (2012). Efficiency comparison of unrelated question models based on same privacy protection degree. Statistical Papers, 53, 987–999. https://doi.org/10.1007/s00362-011-0403-4. →
Greenberg, B. G., Abul-Ela, A.-L. A., Simmons, W. R., & Horvitz, D. G. (1969). The unrelated question randomized response model: theoretical framework. Journal of the American Statistical Association, 64(326), 520–539. →
Groves, R. M., Fowler, F. J., Couper, M. P., Lepkowski, G. M., Singer, E., & Tourangeau, R. (2004). Survey methodology. Hoboken: John Wiley & Sons. a, b
Guerriero, M., & Sandri, M. F. (2007). A note on the comparison of some randomized response procedures. Journal of Statistical Planning and Inference, 137, 2184–2190. https://doi.org/10.1016/j.jspi.2006.07.004. →
Heck, D. W., Hoffmann, A., & Moshagen, M. (2018). Detecting nonadherence without loss in efficiency: a simple extension of the crosswise model. Behavioral Research, 50, 1895–1905. https://doi.org/10.3758/s13428-017-0957-8. →
Hoffmann, A., & Musch, J. (2016). Assessing the validity of two indirect questioning techniques: a stochastic lie detector versus the crosswise model. Behavioral Research Methods, 48, 1032–1046. https://doi.org/10.3758/s13428-015-0628-6. →
Hoffmann, A., Diedenhofen, B., Verschuere, B., & Musch, J. (2015). A strong validation of the crosswise model using experimentally-induced cheating behavior. Experimental Psychology, 62(6), 403–414. https://doi.org/10.1027/1618-3169/a000304. →
Hoffmann, A., Waubert de Puiseau, B., Schmidt, A. F., & Musch, J. (2017). On the comprehensibility and perceived privacy protection of indirect questioning techniques. Behavioral Research Methods, 49, 1470–1483. https://doi.org/10.3758/s13428-016-0804-3. a, b
Hoffmann, A., Meisters, J., & Musch, J. (2020). On the validity of non-randomized response techniques: an experimental comparison of the crosswise model and the triangular model. Behavioral Research Methods, 52, 1768–1782. https://doi.org/10.3758/s13428-020-01349-9. →
Höglinger, M., & Diekmann, A. (2017). Uncovering a blind spot in sensitive question research: false positives undermine the Crosswise-Model RRT. Political Analysis, 25, 131–137. https://doi.org/10.1017/pan.2016.5. a, b
Höglinger, M., Jann, B., & Diekmann, A. (2016). Sensitive questions in online surveys: an experimental evaluation of different implementations of the randomized response technique and the Crosswise Model. Survey Research Methods, 10(3), 171–187. https://doi.org/10.18148/srm/2016.v10i3.6703. →
Horvitz, D. G., Shah, B. V., & Simmons, W. R. (1967). The unrelated question randomized response model. In Proceedings of the Section on Survey Research Methods (pp. 65–72). American Statistical Association. →
Horvitz, D. G., Greenberg, B. G., & Abernathy, J. R. (1976). Randomized response: a data-gathering device for sensitive questions. International Statistical Review, 44(2), 181–196. https://www.jstor.org/stable/1403276. →
Jann, B., Jerke, J., & Krumpal, I. (2012). Asking sensitive questions using the crosswise model: an experimental survey measuring plagiarism. The Public Opinion Quarterly, 76(1), 32–49. https://www.jstor.org/stable/41345966. →
Jerke, J., Johann, D., Rauhut, H., Thomas, K., & Velicu, A. (2022). Handle with care: implementation of the list experiment and crosswise model in a large-scale survey on academic misconduct. Field Methods, 34(1), 69–81. https://doi.org/10.1177/1525822X20985629. a, b
Krause, T., & Wahl, A. (2022). Non-compliance with indirect questioning techniques: an aggregate and individual level validation. Survey Research Methods, 16(1), 45–60. https://doi.org/10.18148/srm/2022.v16i1.7824. →
Krumpal, I. (2012). Estimating the prevalence of xenophobia and anti-Semitism in Germany: a comparison of randomized response and direct questioning. Social Science Research, 41(6), 1387–1403. https://www.sciencedirect.com/science/article/abs/pii/S0049089X12001172. →
Kuk, A. Y. C. (1990). Asking sensitive questions indirectly. Biometrika, 77(2), 436–438. https://doi.org/10.1093/biomet/77.2.436. →
Kundt, T. C., Misch, F., & Nerré, B. (2017). Re-assessing the merits of measuring tax evasion through business surveys: an application of the crosswise model. International Tax and Public Finance, 24(1), 112–133. https://doi.org/10.1007/s10797-015-9373-0. a, b, c
Mangat, N. S. (1994). An improved randomized response strategy. Journal of the Royal Statistical Society, Series B, 56, 93–95. https://www.jstor.org/stable/2346030. →
Meisters, J., Hoffmann, A., & Musch, J. (2020a). Can detailed instructions and comprehension checks increase the validity of crosswise model estimates? PLoS ONE, 15(6), e235403. https://doi.org/10.1371/journal.pone.0235403. a, b
Meisters, J., Hoffmann, A., & Musch, J. (2020b). Controlling social desirability bias: an experimental investigation of the extended crosswise model. PLoS ONE, 15(12), e243384. https://doi.org/10.1371/journal.pone.0243384. →
Meisters, J., Hoffmann, A., & Musch, J. (2022). A new approach to detecting cheating in sensitive surveys: the cheating detection triangular model. Sociological Methods & Research. https://doi.org/10.1177/00491241211055764. →
Moshagen, M., Musch, J., & Erdfelder, E. (2012). A stochastic lie detector. Behavioral Research Methods, 44, 222–231. https://doi.org/10.3758/s13428-011-0144-2. →
Nakhaee, M. R., Pakravan, F., & Nakhaee, N. (2013). Prevalence of use of anabolic steroids by bodybuilders using three methods in a city of Iran. Addict Health, 5(3–4), 77–82. →
Peeters, C. F. W., Lensvelt-Mulders, G. J. L. M., & Lasthuizen, K. (2010). A note on a simple and practical randomized response framework for eliciting sensitive dichotomous and quantitative information. Sociological Methods & Research, 39(2), 283–296. https://doi.org/10.1177/0049124110378099. →
Perri, P. F., Manoli, E., & Christofides, T. C. (2022). Assessing the effectiveness of indirect questioning techniques by detecting liars. Statistical Papers. https://doi.org/10.1007/s00362-022-01352-6. a, b
Quatember, A. (2009). A standardization of randomized response strategies. Survey Methodology, 35(2), 143–152. https://www150.statcan.gc.ca/n1/pub/12-001-x/2009002/article/11037-eng.pdf. →
Quatember, A. (2012). An extension of the standardized randomized response technique to a multi-stage setup. Statistical Methods & Applications, 21(4), 475–484. https://doi.org/10.1007/s10260-012-0209-0. →
Quatember, A. (2014). A randomized response design for a polychotomous sensitive population and its application to opinion polls. Model Assisted Statistics and Applications, 9(1), 11–23. https://doi.org/10.3233/MAS-130275. →
Quatember, A. (2019). A discussion of the two different aspects of privacy protection in indirect questioning designs. Quality & Quantity, 53, 269–282. https://doi.org/10.1007/s11135-018-0751-4. a, b
Särndal, C.-E., Swensson, B., & Wretman, J. (1992). Model-assisted survey sampling. New York: Springer. a, b, c
Schnapp, P. (2019). Sensitive question techniques and careless responding: adjusting the crosswise model for random answers. methods, data, analyses, 13(2), 307–320. https://doi.org/10.12758/mda.2019.03. →
Schnell, R., & Thomas, K. (2023). A meta-analysis of studies on the performance of the crosswise model. Sociological Methods & Research, 52(3), 1493–1518. https://doi.org/10.1177/0049124121995520. a, b
Soeken, K. L., & Macready, G. B. (1982). Respondents’ perceived protection when using randomized response”. Psychological Bulletin, 92(2), 487–489. →
St John, F. A., Keane, A. M., Edwards-Jones, G., Jones, L., Yarnell, R. W., & Jones, J. P. (2012). Identifying indicators of illegal behaviour: carnivore killing in human-managed landscapes. Proceedings of the Royal Society B: Biological Sciences, 279, 804–812. https://doi.org/10.1098/rspb.2011.1228. →
Tan, M. T., Tian, G.-L., & Tang, M.-L. (2009). Sample surveys with sensitive questions: a nonrandomized response approach. The American Statistician, 63(1), 9–16. https://doi.org/10.1198/tast.2009.0002. →
Tian, G.-L. (2014). A new non-randomized response model: the parallel model. Statistica Neerlandica, 68(4), 293–323. https://doi.org/10.1111/stan.12034. a, b, c, d
Tian, G.-L., & Tang, M.-L. (2014). Incomplete categorical data design. Non-randomized response techniques for sensitive questions in surveys. Boca Raton: CRC Press. →
Tian, G.-L., Tang, M.-L., Wu, Q., & Liu, Y. (2017). Poisson and negative binomial item count techniques for surveys with sensitive question. Statistical Methods in Medical Research, 26(2), 931–947. https://doi.org/10.1177/0962280214563345. →
Tourangeau, R., & Yan, T. (2007). Sensitive questions in surveys”. Psychological Bulletin, 133(5), 859–883. https://doi.org/10.1037/0033-2909.133.5.859. →
Walzenbach, S., & Hinz, T. (2019). Pouring water into wine: revisiting the advantages of the crosswise model for asking sensitive questions. Survey Methods: Insights from the Field.. https://doi.org/10.13094/SMIF-2019-00002. →
Walzenbach, S., & Hinz, T. (2023). Puzzling answers to crosswise models: examining overall prevalence rates, response order effects, and learning effects. Survey Research Methods, 17(1), 1–13. https://doi.org/10.18148/srm/2023.v17i1.8010. →
Warner, S. L. (1965). Randomized response: A survey technique for eliminating evasive answer bias. Journal of the American Statistical Association, 60, 63–69. https://www.jstor.org/stable/2283137. →
Waubert de Puiseau, B., Hoffmann, A., & Musch, J. (2017). How indirect questioning techniques may promote democracy: a preelection polling experiment. Basic and Applied Social Psychology, 39(4), 209–217. https://doi.org/10.1080/01973533.2017.1331351. →
Wolter, F., & Diekmann, A. (2021). False positives and the ‘more-is-better’ assumption in sensitive question research: new evidence on the crosswise model and the item count technique. Public Opinion Quarterly, 85(3), 836–863. https://doi.org/10.1093/poq/nfab043. a, b
Yu, J.-W., Tian, G.-L., & Tang, M.-L. (2008). Two new models for survey sampling with sensitive characteristic: design and analysis. Metrika, 67, 251–263. https://doi.org/10.1007/s00184-007-0131-x. a, b, c, d, e, f