Worst Case Resistance Testing: A Nonresponse Bias Solution for Today’s Survey Research Realities

1 Introduction

All quantitative empirical methods rely on the assumption that the sample participants represent the population of interest sufficiently to justify extrapolation of findings beyond the sample measured (Chesney & Obrecht, 2012). However, some portion of the participants solicited in almost every study do not respond, and as the proportion of those nonrespondents grows larger, the study’s results suffer from potential bias (Boyd & Westfall, 1965). This participant nonresponse bias is the focus of this paper.

Participant nonresponse bias has been attributed to the variation of characteristics between respondents and nonrespondents (Deming, 1953), and this variance has the potential to confound the variance observed between the constructs measured in any given empirical test (Groves and Peytcheva, 2008) and introduce bias into statistical tests. This bias can be thought of as a type of selection bias and unlike bias for nonresponse of individual items this bias cannot be corrected without gathering data from nonrespondents (Berg, 2005).

The growing use of internet surveys for behavioral survey research has changed the nature of survey response and nonresponse. While scholars have well accepted means of assessing nonresponse bias—most notably, wave analysis—those methods were developed based upon physical mail collection of surveys. By contrast, much survey and experimental research today employs electronically curated samples that can be gathered in hours, or even minutes and that does not have well defined participant response data.

Accordingly, this study develops a set of methods independent of the survey delivery mode, allowing researchers to examine the robustness of statistical tests against participant nonresponse bias¹ by calculating the number of cases needed to reverse a statistical test over a range of different effect sizes. The resulting “n-curves” provide similar insight to related methods, such as power curves and p‑curves, and provide a measure of robustness for the results of statistical tests in situations where participant nonresponse may affect the results and conclusions from such tests. Monte Carlo experiments are used to test the properties of the proposed method across multiple statistical tests. An empirical survey of customer satisfaction is then used to show how these methods can be used on their own or combined with wave analysis to flag statistical tests where nonresponse bias may be problematic. The data files and code used in the creation of this paper have been made available (France et al., 2024a, b).

2 Background

In recent years, dedicated efforts have examined practices such as “p-hacking” to recall the academy to replicable research methods (Simmons et. al, 2011). Similarly, recent failures to replicate psychological research have been a cause for concern (Stanley et al., 2018), leading to a call for more transparency in research (Inman et al., 2018). This includes the reporting of data collection techniques, statistical power, effect sizes, and potential biases that might influence results.

Arising from a combination of sampling error and coverage error, nonresponse error results in a sufficient difference between the data sought by a researcher and the data actually obtained to compromise a study’s validity (Collier & Bienstock, 2007). Conceptually, nonresponse error holds that the potential responses of subjects who do not answer a solicitation to participate in a given research study might be different enough from the responses recorded to alter the findings of the study and higher nonresponse rates can negatively affect the representativeness of a sample (Cook et al., 2000). When records of response data are available, it is quite easy to assess participant nonresponse, but “there is no magical response rate below which an observed mean, standard deviation, or correlation becomes automatically invalid” (Newman 2009, pp. 7). Still, the larger the percentage of the solicited sample measured, the lower the error resulting from nonresponse bias tends to be (Olson, 2006).

Scholars have developed several procedures to adjust survey results to account for survey nonresponse bias, as detailed in Table 1 (following Halbesleben & Whitman, 2013), but they all inherently rest on a key assumption: “… respondents and nonrespondents within a weighting class have the same values on key variables …” (Groves 2006, pp. 653). Accordingly, attempts to assess nonresponse bias rely on an assumption that differences causing some solicited subjects to forego answering a survey are related to how a nonrespondent might react to a study’s constructs of interest. Based on this assumption, for decades, the most widely used method of assessing nonresponse bias has been Armstrong and Overton’s wave analysis technique (1977).

2.1 Covariate Methods

Several of the listed methods in Table 1 utilize covariate information in order to account for differences between the sample and the solicited respondents. Methods include weighting using correlations with covariates (Wetzel & Hünteler, 2022), propensity score methods (Lee, 2006; Schonlau et al., 2009), and methods that utilize feasible ranges of covariate information to create selection bias functions for parameter estimation (Rotnitzky et al., 1998, Scharfstein & Irizarry, 2003) and for creating solution bounds (Horowitz & Manski, 1998; Manski, 2016). These methods can be particularly useful in longitudinal data collection, where subject covariates are known, but subjects may miss measurement occasions or drop out of an experiment.

2.2 Wave Analysis

Simply put, wave analysis compares relationships between variables observed among early respondents to a measurement instrument with those observed among later respondents (Armstrong & Overton, 1977). “The basic assumption … is that subjects who respond less readily are more like those who do not respond at all than those who do respond readily (i.e., those who respond sooner and those who need less prodding to answer)” (Kanuk & Berenson, 1975, pg. 449). The method poses that a lack of significant difference between early and late respondents to a research solicitation implies that potential subjects that did not respond do not represent observations that might alter an analysis’s results.

For all its long-proven utility (over 21,000 citations at this writing), wave analysis was explicitly built around mail surveys, which generally require considerable periods of time to collect (Kanuk & Berenson, 1975) and where information on early and late response waves can easily be found. Studies employing postal mail and citing wave analysis have included follow up prompts of up to four weeks (Diamantopoulos & Winklhofer, 2001; Mohr & Spekman, 1994; Sirdeshmukh et al. 2002). Even surveys distributed over email have noted significant time spent waiting for responses from subjects (Pavlou, 2003). As of 2020, the vast majority of surveys were completed via the internet (Daikeler et al., 2020). The “internet age” of surveys has seen a growth of third-party survey platforms, such as Qualtrics and Prolific, who recruit participants well in advance of any study, and pay participants fees to complete studies. The resulting participants are more likely to reply quickly because they have pre-agreed to participate in studies (Qualtrics, 2020). On some research platforms, such as Prolific (Peer et al., 2017) and the Amazon Mechanical Turk (Chandler et al., 2019), potential respondents, when logging on, will pick from a list of potential surveys or work to complete. In this situation, unless user click/screen viewing behavior is analyzed, it is difficult to identify and quantify nonresponses (e.g., Boas et al., 2020; Paolacci et al., 2010) and the early and late response waves required by wave analysis.

2.3 Resampling

A typical means of addressing potential nonresponse bias is to simply resolicit sample nonrespondents (Aiken, 1981; Hartman et al., 1986; MacDonald et al., 2009), often employing shorter surveys that assess only the items whose constructs are of critical importance to the observed findings, to look for differences from the findings of the original survey (Lambert & Harrington, 1990). However, the absence of a specific response rate below which nonresponse bias is considered problematic (Newman, 2009) implies that supplemental sampling—whether among the originally solicited group, or from a different group of potential respondents—may not necessarily address nonresponse bias of a sample relative to the population of interest. A different potential solution may lie in using meta-analysis techniques to address a bias issue known as the file drawer problem.

2.4 Meta-Analysis and the File Drawer Problem

The file drawer problem is a term used in meta-analytic literature to describe a conceptual, but quantifiable sampling bias. Because meta-analyses examine the standardized results of extant literature, they are presumed to be biased by the tendency of statistically significant findings to achieve academic publication, and the corollary tendency of non-significant results of similar phenomena never entering the scholarly body of knowledge (Rosenberg, 2005). The worst assumptions hold that 95% of contrary findings do not survive the academic publication process, and that the body of knowledge is, therefore, a victim of Type 1 error (Rosenthal, 1979).

Rosenthal (1979) proposed a solution to the file drawer problem, sometimes known as worst-case resistance testing, or fail-safe number calculation (Rosenberg, 2005). The technique calculates the number of studies required to significantly alter an observed mean of effect sizes, assuming the hypothetical unobserved studies have a collective mean significantly different than that of the observed effect sizes. As this calculated number of studies increases, the likelihood of a file drawer bias decreases. In other words, the larger the effect size observed in tests of a given sample, and/or the less stringent the standard of testing significance, the more hypothetical contradictory cases it would take to cast doubt on the observed findings. The technique has been used in varying meta-analytic studies including (but by no means limited to) electronic word of mouth (Babić et al., 2016), interstitial space impacts on consumer appeal (Sevilla & Townsend, 2016), and consumer responses to humanoid robots (Mende et al., 2019).

The nonresponse bias problem is very similar to the file drawer problem in that both seek to assess a difficult-to-quantify bias of findings stemming from uncollected data presumed to contradict results based on observed data. It stands to reason that the file drawer or worst-case resistance testing (WCRT) solution should also be efficacious in assessing nonresponse bias.

3 Methodology

To illustrate how file drawer concepts can be applied to the nonresponse bias problem, the problem is given in general in terms of the basic NHST (null hypothesis significance test) paradigm. Though this paradigm has been much criticized (e.g., Gill, 1999; Hubbard & Armstrong, 2006; Hunter, 1997; Schneider, 2015) it is still by far the predominantly used framework for building theory in empirical management and social science research.

Furthermore, most alternative approaches proposed to replace NHST also have criticisms. For example, the use of confidence intervals for inference leads to the same “inverse inference” that is criticized in NHST testing, and Bayesian analysis requires specification of prior distributions, which can be conceptually difficult (e.g., Trafimow, 2017). While at least one journal has banned significance testing (Woolston, 2015), most journals and scientific associations in the behavior sciences and business disciplines have focused on best practice to improve the use of NHST results and to put these results into context.

Scholars have advanced several recommendations to improve the implementation of NHST methods. These include putting p values into context and avoiding erroneous overly strong conclusions from p values (Wasserstein & Lazar, 2016), focusing on the magnitude and size of any statistical effect and incorporating information from prior beliefs using Bayes factors (Harvey, 2017; Valentine et al., 2019), reporting of descriptive statistics and reporting guidelines for major statistical tests (JCR, 2021), including detailed graphs and discussions of effects and utilizing robust error statistics (Schwab et al., 2011), and calculating power values for each statistical test and ensuring that the Type II error rate (β) is less than 0.05 when making conclusions on a lack of “effect” relative to a null hypothesis (Baroudi & Orlikowski, 1989; Cashen & Geiger, 2004).

A theme in most of the rules and suggestions described above is the “triangulation” of NHST results with other metrics to build evidence for hypothesis test conclusions. As such, the methodology described in this paper fits in with this theme. The aim is to provide a set of measures of robustness of statistical results to problems caused by nonresponse bias. However, the methods described can be used beyond the realm of nonresponse bias to examine robustness to other sources of error, such as the experimental design.

In this study, the WCRT methodology is described using a generic NHST hypothesis testing procedure. Examples are included for problems with simple hypothesis testing of means and of correlations, where equations are given for “finding the number of additional studies” required to negate a conclusion and then models are developed to solve these equations.

3.1 The General Model

A researcher will often make the “opposite assertion”, that given insufficient evidence to reject H₀, one can conclude that H₀ is in fact true. However, there is a danger with this assertion in that researchers may assume a trivial effect without understanding the implications of the power of the statistical test (Baroudi & Orlikowski, 1989; Cashen & Geiger, 2004; Sawyer & Ball, 1981). If the researcher fails to reject H₀ and in fact H_A is true, then the researcher has made a Type II error, i.e., $\beta =P\left(R^c\left(H_A\right)\right)$, where the power of the test is 1−β. An issue here is that H_A can take multiple values and that the power varies with the “effect size” difference between H₀ and the H_A used to calculate power. Solutions to this issue include calculating power using a reasonable effect size based on prior studies, standard small, medium, and large effect sizes (Cohen, 1992), and graphing power values across a range of effect sizes, a “so called” power curve (Faul et al., 2007).

In the context of nonresponse bias and WCRT, the focus is to find the number of nonrespondents who can reverse a statistical conclusion and use this as a measure of robustness of the solution. But how is the effect size for these studies chosen? Is it a “zero effect”, the opposite effect, or a smaller effect in the same direction? The methodology outlined in this paper mirrors the work described above in choosing effect sizes for power analyses. The number of nonrespondents needed to reverse a statistical test can be calculated for a range of feasible effect sizes, which can be estimated from wave analysis or by examining effect sizes for similar studies. These values can be plotted, creating an “n curve”, which is similar to curves used for determining quality bounds for confidence intervals (e.g., Trafimow, 2018) or p‑curves used to map sample sizes for different p values at different power levels (Simonsohn et al., 2014).

At the core of the analyses in this paper is the idea of a standardized effect size (Cohen, 1988). An effect size can be thought of as a quantitative measure of the phenomenon being studied (Kelley & Preacher, 2012). For example, for a single sample t test, the effect size d, is given in (1).

where $\bar{x}$ is the sample mean, s is the sample standard deviation, μ₀ is the hypothesized population mean, and n is the sample size. This invariance towards n is particularly useful for large sample size experiments, as effect sizes can put into context results that are statistically significant with only a small effect size, but a very large sample size (e.g., Coe, 2002). Different statistical tests have different effect size calculations. For example, effect sizes for the comparison of two group means, such as Cohen’s d and Hedge’s g, have a similar format to the effect size given in (1), while for Pearson’s correlation, the sample regression coefficient r is often used as a measure of effect size (Hemphill, 2003).

In the context of a WCRT analysis of a NHST test, we define a general effect size φ, which can be substituted by the appropriate metric for a specific test (e.g., d for a sample mean test). Consider the following situations:

1. 1.

   With a sample size of size n₁ and effect size φ₁ there is enough evidence to reject H₀. We wish to find n₂, where this is the number of items or nonrespondents with effect size φ₂ required to negate the result, so that H₀ is no longer rejected.

2. 2.

   With a sample of size of n₁ and effect size φ₁, there is not enough evidence to reject H₀. We wish to find n₂, where this is the number of items or nonrespondents with effect size φ₂ required to negate the result, so that H₀ is now rejected.

A set of candidate effect sizes needs to be defined for φ₂. This is key to the methods described in this paper and the appropriate range can be informed by previous research, the results from a wave analysis of the data, and the effect size φ₁ (for example, if there is a significant effect, an effect size greater or equal to φ₁ and in the same direction is not going to negate the hypothesis test). For each φ_2, the procedure will give the n₂ value needed to reverse the result of the statistical test.

3.2 Inference for Single Sample t test

Consider a single sample t test of a population mean being equal to hypothesized mean μ₀. The notation is as per (1) and the null hypothesis is $H_o:\mu ={\mu }_0$. The methodology outlined in this section covers both two tailed tests where the alternative hypothesis is defined as $H_a:\mu \ne {\mu }_0$ and one-tailed tests where the alternative hypothesis can be defined as $H_a:\mu >{\mu }_0$ or $H_a:\mu <{\mu }_0.$ The test statistic derived from the sampling distribution is defined as (2) by rearranging (1).

Here, the subscript 1 indicates that the sample values are based on the responses, while the subscript 2 will be used for the sample values for hypothesized nonresponses. The t distribution has n-1 degrees of freedom and varies with n. Let $t^{*}$ be the critical boundary between rejecting and failing to reject H₀. Dependent on n and the strictness of the test (using the Type I error α), H₀ is rejected if $\left(t\right)>t^{*}=t_{\alpha /2}$ for a two-tailed test and $t>t^{*}=t_{\alpha }$(or $t<t^{*}={-t}_{\alpha }$) for a one-tailed test.

Here we consider four different scenarios².

1. 1.

   For a one-tailed upper test or a two-tailed test with $t>0,$ H₀ is rejected as $t>t^{*}$. We wish to find, for some nonrespondents with effect size d₂, the n₂ for required to reverse this conclusion, so that $t\le t^{*}$.

2. 2.

   For a one-tailed upper test or a two-tailed test with $t>0,$ H₀ is not rejected as $t\le t^{*}$. We wish to find, for some nonrespondents with effect size d₂, the n₂ required to reverse this conclusion, so that $t>t^{*}$.

3. 3.

   For a one-tailed lower test or a two-tailed test with $t<0,$ H₀ is rejected as . We wish to find, for some nonrespondents with effect size d₂, the n₂ required to reverse this conclusion, so that $t\ge t^{*}$.

4. 4.

   For a one-tailed lower test or a two-tailed test with $t<0,$ H₀ is not rejected as $t\ge t^{*}$. We wish to find, for some nonrespondents with effect size d₂, the n₂ required to reverse this conclusion, so that .

A simplifying assumption is to assume that $s_1=s_2$, i.e., the nonresponse and response data have the same standard deviations. However, if the nonresponse data have different characteristics than the original data then this assumption will not hold. A solution is to set some range for s₂, so that $\left(1-\theta \right)s_1\le s_2\le \left(1+\theta \right)s_1$, where $0\le \theta \le 1$ and θ is set based on some prior inferences regarding the data. Given s₂, the effect size for the nonresponse data is given in (3).

The sample mean for the nonresponse data is found by rearranging (3) to give (4).

This value can be used to find the sample mean for the combined response and nonresponse samples.

The pooled standard deviation can be calculated using the meta-analysis formulation given in Higgins et al. (2019).

Consider the overall t test with the combined data for scenario 1. We wish to find the lowest n₂ for which $t\le t^{*}$, and define some small quantity ε, such that $t+\epsilon =t^{*}$, with $\epsilon \ge 0$, so that $t=t^{*}-\epsilon$.

Utilize to expand out ${\bar{x}}_c$ in terms of n₁ and n₂.

Multiply both the numerator and denominator by n₁ + n₂ and then rearrange the numerator terms.

The task is to find the smallest integer value of n₂ for which $\epsilon \ge 0$. By making minor alterations, (9) can be used for scenarios (2)–(4). The four scenarios are summarized in Table 2.

For each scenario, Table 2 gives the test direction (upper or lower), the result of the test on the response data, the opposite result, the range of ε for which the minimum integer n₂ is being found, and how the nonresponse effect size is bounded³. Given that the t‑value in (9) is dependent on n₂, giving a cross-dependency, n₂ cannot be calculated directly. A fixed-point optimization procedure for finding n₂ is given in Appendix A. An almost identical procedure can be used for the single sample z test.

A similar process can be followed for two-sample independent sample tests. Sample sizes can be calculated for Student’s t test (for equal variances), Welch’s t test (for unequal variances), and the two sample z test. A two-group measure, such as Hedge’s g or Cohen’s d can be used to calculate effect sizes (Rosenthal & Rubin, 1982). If sample sizes are uneven, some constraints need to be placed on relative group sizes. Derivations for the two-sample tests are included in Appendix B.

3.3 Inference for Correlation Test

Consider a situation where a correlation is being tested for significance. The null hypothesis is $H_o:\rho =0$, where ρ is the population correlation. Standard alternate hypothesis are $H_a:\rho >0$ (or ) for a one-tailed test and $H_a:\rho \ne 0$ for a two tailed test. A population hypothesis is tested with a Pearson sample correlation coefficient r. The correlation r is essentially an effect size (Cohen, 1988), with small ($0.1\le r<0.3$), medium ($0.3\le r<0.5$), and large ($r\ge 0.5$) effect sizes defined.

There are several different tests for the significance of correlations. The one most commonly used in meta-analysis involves transforming the correlation $r\in \left(-\mathrm{1,1}\right)$ into a z score using the inverse hyperbolic tangent transformation (Cox, 2008) and is given in (10).

where r₁ is the correlation coefficient for the response data. Now, this value is still essentially an effect size and does not depend on the sample size n. A standard error of $\sqrt[]{1/\left(n-3\right)}$ is defined by Fisher (1921), which can be used to give the z statistic in (11).

Given that the z test is a simple two-way directional test, the four scenarios for finding the n₂ values needed to change a hypothesis test result are similar to the scenarios outlined for the one sample t test in Table 2. The only changes are that “z” replaces “t” for the test statistic and critical values, and that the effect size defined for the nonresponse data is a correlation coefficient r₂, which can be transformed into a z score zr₂ using the transformation given in (10). The z‑scores for the response and hypothesized nonresponse data can be combined (Field, 2001; Hedges & Vevea, 1998; Higgins et al., 2019) using (12).

which has the standard error given in (13).

For scenario 1, we wish to find the lowest n for which $z\le z^{*}$, where $z^{*}$ is the boundary value for significance and define some small quantity ε, such that $z+\epsilon =z^{*}$, with $\epsilon \ge 0$, so that $z=z^{*}-\epsilon$.

This equation can be rearranged to give n₂.

Now, n₂ can be found in a similar manner to the single sample hypothesis test. The other three scenarios can be taken from Table 2 (with r replacing d in the final column). A local search optimization procedure for finding n₂ is given in Appendix A.

4 Monte Carlo Simulations

To help validate the methods described in the previous section, several Monte Carlo simulation experiments were run. The methods outlined in this article are not “supervised” in the traditional sense, in that they give an analytical measure of resiliency rather than an ex-ante prediction of a dependent variable. However, the methods can be evaluated in a similar manner to evaluations of unsupervised analysis, for example, cluster analysis. Here, the method assumptions and the results generated by the method are tested on error-perturbed input data, to see how the resilient the model is to error. This approach has been widely used in dimensionality reduction (e.g., Akkucuk & Carroll, 2006; Chen & Buja, 2009) and cluster analysis (e.g., Banfield & Raftery, 1993; Brusco et al., 2017; Milligan, 1981). For example, in cluster analysis, one can generate items for clusters with Gaussian error from the cluster centroids and then see how well items are assigned to the correct clusters. We followed this approach and generated a range of data distributions for each of the tested WCRT methods, varying the factors of the sample size, the error distribution, the test coefficient, the sample data effect size, and the opposing WCRT (nonrespondent) effect size. The factors and factor levels in the experimental design are summarized in Table 3.

Regardless of the statistical test, the general properties of the WCRT methodology outlined in the previous section should give estimates with the following causal relations for significant statistical tests (in each case holding all other variables constant).

• Property 1: As the sample size n increases, the WRCT n should increase (as more evidence is required to reverse the test result).

• Property 2: As the value of α increases, the WRCT n to reverse the result should increase (as hypothesis test boundary is closer to the center of the H₀ distribution).

• Property 3: As the overall sample data effect size for the sample increases, the WRCT n to reverse the result should increase (as the sample effect is stronger).

• Property 4: As the file drawer WRCT (opposing) effect size increases, the n to reverse the result should decrease (as the items in the opposing sample are more strongly opposing the test result).

In a full factorial design, for each combination of factor levels, 10 random samples were taken, giving a total of 259,200 experimental runs. For each solution, an effect size was taken and then random error was added for each of the items in the generated data. The random error was generated from the stated distribution (normal, uniform, Poisson, or negative exponential) and scaled to give a mean of 0 and standard deviation of 1 (as the error is relative to a standardized effect size).

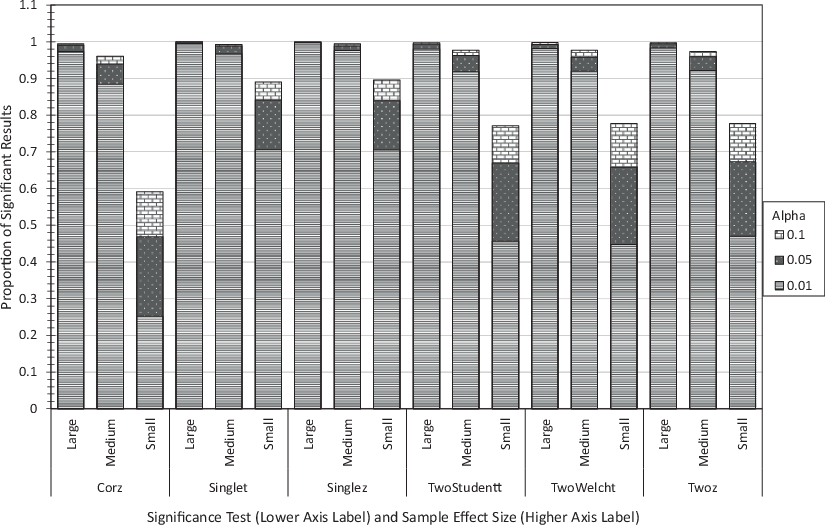
As an initial test of experimental procedure and as a manipulation check, the proportion of significant tests was summarized for each combination of test and effect size (small, medium, and large). The resulting bar graph is given in Fig. 1. As the proportion of significant results increases as the hypothesis tests become less strict with higher α, results are overlaid for the different values of α, with the smallest values of α plotted at the front. As expected, for every test, the proportion of significant results is monotone increasing with the sample data effect size.

Fig. 1 The Proportion of Significant Results by Test, Effect Size, and Alpha (α)

Further analyzing the significant test results (n = 225,635), summary graphs were produced to illustrate the properties outlined in points 1–4. Fig. 2 gives the WRCT n required to reverse significance given across all combinations of sample data effect size and opposing WRCT effect size. Each bar is for a WRCT file drawer effect size (higher axis description) and three values of α. As per Fig. 1, lower values of α are plotted at the front. The bars are grouped by the sample data effect size (lower axis description). Once can see that as alpha (α) increases, the WRCT n increases, giving evidence for Property 2. As the sample effect size increases, the WRCT n increases, giving evidence for Property 3, and as the WCRT file drawer effect opposing effect size increases, the WRCT n decreases, giving evidence for Property 4.

Fig. 2 The File Drawer Number of Studies to Negate Significance Across Different Effect Sizes and Alpha (α) Values

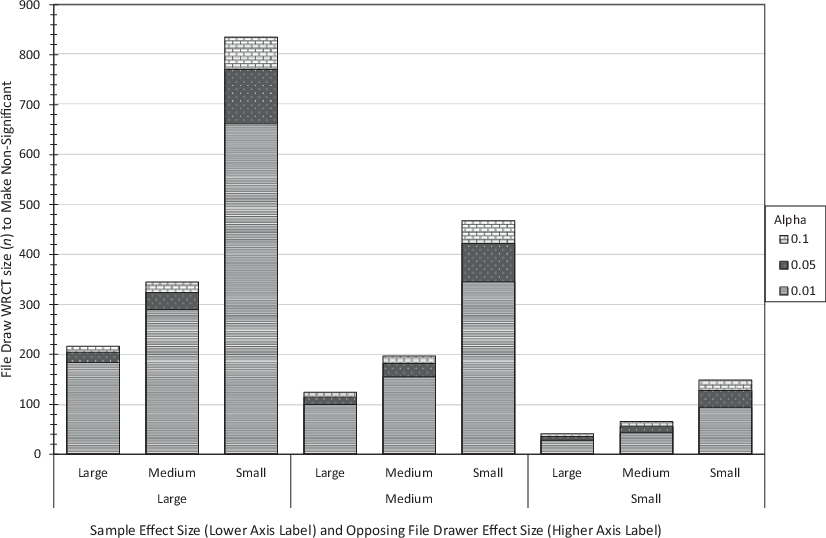
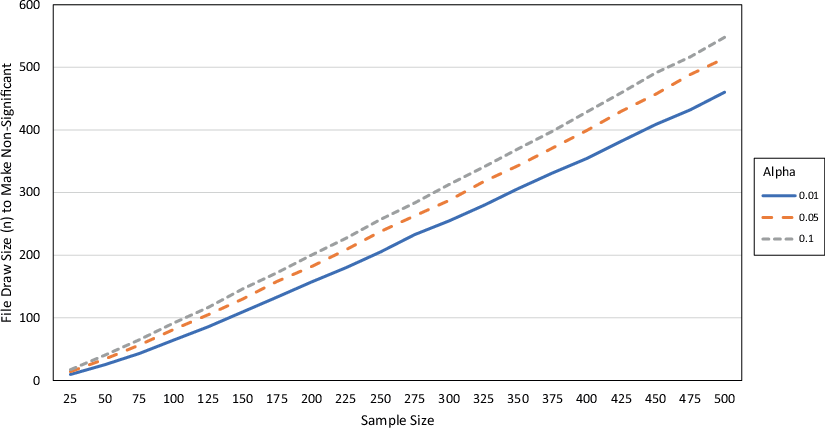
Fig. 3 gives the WRCT n required to reverse significance given across all values of alpha (α) and all combinations of data sample size. As with Fig. 2, as alpha (α) increases, the WRCT n increases, giving evidence for Property 3. There is a positive relationship between the data sample size n and the WRCT n, giving evidence for Property 1. From the previous analytic work, the relationship should be linear, as the WRCT n is linearly related to the sample size n. There is a small deviance from linearity due to the error added to the data, but the overall relationship still strongly holds.

Fig. 3 The File Drawer Number of Studies to Negate Significance Across Different Sample Sizes and Alpha (α) Values

To further understand the effect of the experimental factors, an OLS regression was run with the WRCT n as the dependent variable and the experimental factors as the independent variables. As the sample data effect could be either positive or negative, this variable was split into the direction (positive or negative) and the size of the effect. A regression with main effects and a regression that also included two factor interactions were run. The addition of two-factor interactions only improved the model fit slightly, so for the sake of parsimony the simpler main effect model was reported. All variables apart from the direction and error distribution were significant. These variables were removed from the model. For the direction, this behavior is expected as a negative data sample effect and a positive WCRT effect size should give the same WCRT n as a positive data sample effect and a negative WCRT effect size with the same magnitudes. The different error distributions were tested to show the robustness of the WCRT procedure with different types of error. However, these do not strongly affect the performance. It may be that for larger sample sizes the central limit theorem makes the actual error distribution unimportant. The results are reported in Table 4. The reference levels are “Small” for the sample data and WRCT effect sizes, alpha (α = 0.01) for the significance level, and the Correlation z test for the test. The overall R² is 0.6989, indicating a strong fit, through with some variability due to the error added to the sample datasets.

In line with the model free evidence in the graphs, the WRCT n increases as the sample size increases, as the sample data effect size increases, and as the alpha increases. This gives additional evidence for Properties 1 to 4. The statistical test factor is significant, but this only gives evidence that the different statistical tests require different WRCT n values to reverse significance relative to the other experimental factors, which is to be expected. Overall, the tests show that the WRCT procedure works as expected and is robust to error variance in the sample data.

4.1 Simulation Experiment for Regression Data

This section demonstrates the use of the framework for regression. A real world dataset was taken from Hernán & Robins (2020), which contains cleaned data for the National Health and Nutrition Examination Follow-up Study (NHEFS). The data can be utilized for regression analysis, where the purpose is to explain and predict a subject’s cholesterol level from a range of demographic and health indicators, including height, weight, blood pressure, gender, age, income, smoking habits, alcohol consumption, and exercise levels. The utilized dataset in total had 12 predictors and 1461 complete rows of data. Here, the fact that OLS regression generates a correlation variable is exploited to give a measure of robustness for OLS regression⁴.

It can be assumed that as more predictors are added to an OLS regression model the R² value and thus the correlation (r) will increase. As with the previous experiment, larger values of the (opposite) WRCT effect size will give smaller WRCT n robustness values and larger values of the Type I error (α) will give larger WRCT n robustness values. To test these properties, the model was built with each possible combination of predictors. To simulate potential sources of error variance, each dataset was sampled with replacement in a similar manner to how bootstrapping is used to measure error variance on survey data (e.g., Sitter, 1992). In total, given the twelve regression predictors, three potential values of the WRCT effect size (all $r=\sqrt[]{R^2}$ are positive measures of effect size, so only negative small, medium, and large opposing WRCT effects were used), and three values of α, there were $2^{12}\times 3\times 3=\mathrm{36,864}$ experimental conditions. Each experimental condition was run with five replications. The resulting correlation and the opposing WRCT effect size were used to calculate the WCRT n measure of robustness.

All experimental runs apart from runs with models with no predictors and models with only income as a predictor were significant. The significant results aggregated across the number of predictors and the opposing WCRT effect size (r₂ = −0.1 (small), −0.3 (medium), −0.5 (large)) are given in Fig. 4. Here, as expected, the WRCT n measure of robustness increases on aggregate with the number of predictors and decreases with the size of the opposing WCRT effect size (with larger effect sizes plotted at the front).

Fig. 4 The File Drawer Number of Studies to Negate Significance For Regression on Health Data Across Number of Predictors and Alpha (α)

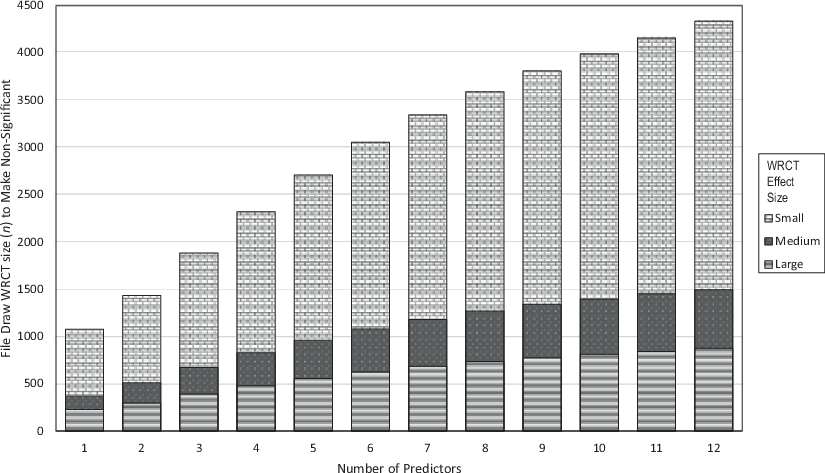
To further test the effect of the predictors, an OLS regression was run with the WCRT (n) as the dependent variable and the predictor presence (0 or 1) for the regression predictors, Type I error (α), and WCRT effect size as independent variables. As expected (Property 4), and in line with Fig. 4, the WRCT (n) is monotone decreasing with the WRCT effect size. In addition, as the value of α increases, making the tests less strict, the value of WRCT (n) required to reverse the tests also increases (Property 2). Every single one of the presence variables is positive, which is in line with expectations, as each additional variable added has a positive effect on the model fit (e.g., one can always set a variable coefficient to 0 and get an identical fit to the model without the variable). Overall, the R² of the model is 0.8665, indicating a strong fit, but with some error variance due to the bootstrap sampling (Table 5).

In summary, Monte Carlo experiments have been utilized to test that the assumed properties (Properties 1–4) of the WRCT (n) measure of robustness hold under situations where data are noisy, and they are robust to error from different error distributions. In addition, the measures can be used as a “heuristic” measure in regression contexts to examine model robustness.

5 Empirical Example

To assess the efficacy of the proposed WCRT method in a survey context, a simple survey was administered to a sample curated through Qualtrics. The goal of the survey was not to investigate any substantive empirical point, but to apply WCRT methods to assess robustness to participant nonresponse bias for a series of correlation tests. As the retailing constructs and scales summarized by Szymanski & Henard (2001) have been widely applied and pose relatively simple questions, they were judged as liable to provide stable results, and unlikely to represent confounding factors due to their complexity.

5.1 The Dataset

The survey includes five different multi-item measurement scales, each of which relates to some measure of customer satisfaction for a recent retail transaction. Each of the individual items is measured using a seven-point Likert scale. The full list of scales and items within these scales is given in Table 6. Overall, there are five different scales, consisting of 19 subitems. The first three scales deal with the actual shopping experience being evaluated, the fourth scale examines how this experience impacts behavioral intent, and the fifth is a general scale measuring retail/shopping enjoyment. Thus, the first three scales should be strongly correlated, while scale five may have some positive correlation with the other scales (someone who has positive views of retail shopping is more likely to select a positive shopping experience), but the level of correlation should be lower. Two of the items (item two on INTENT and item one on ENJOY) were negative direction items and were reversed.

The data were collected via a Qualtrics panel. There were n = 415 fully completed surveys out of a total of n = 463 surveys. In line with the focus on participant nonresponse bias, participant responses with missing items were removed rather than imputed using a missing data technique.

5.2 Exploratory Data Analysis

As a preface to analyzing the correlation tests using WCRT, some analysis was performed on the consistency of the rating scale and on the correlations. To examine the consistency of the summated ratings scales, Cronbach’s alpha (Cronbach, 1951), was calculated for each of the summated rating scales. The values are EXP (0.96), SAT (0.99), PWM (0.96), INTENT (0.78), and ENJOY (0.78). From past literature (e.g., Bland & Altman, 1997; Tavakol & Dennick, 2011), cut-offs for “good” to “excellent” values of alpha range from 0.7–0.95, so these values are in the correct range.

A summary matrix plot of the overall correlations between the values in the summated rating scales is given in Fig. 5. Here, the diagonal values give histogram distributions of the summated values, the upper triangle of the matrix contains the correlations between the summated values (*** represents p < 0.001 for a statistical test of correlation), and the lower triangle contains scatterplots, each overlaid with a linear regression best fit line and a confidence circle for the multivariate mean of the distribution.

Fig. 5 Multi-Item Scale Correlations

5.3 Wave Analysis

The wave analysis approach described in Armstrong and Overton (1977), considers two different waves of responses, an early wave and a late wave, and then a “virtual” wave of nonresponses. While the responses to the survey were not split into waves, for the purpose of this illustrative example, it was assumed that the first 50% belong to the early wave and the second 50% belong to the late wave. The three response scenarios give the number of participant responses for the third wave as 415 (50% response), 1245 (25% response), and 3735 (10% response). Armstrong and Overton (1977) give three methods for calculating values for the third (nonresponse) wave. These are adapted into an effect size context below.

1. 1.

   Assume that the nonresponses have the same effect size as the second wave.

2. 2.

   Assume that the nonresponses have the same effect size as the responses at the end of the second wave.

3. 3.

   Assume a linear interpolation through the nonresponse third wave.

For the measure of interest, let the effect sizes for waves one and two respectively be φ₁ and φ₂. The number of item values in the three waves are denoted n₁, n₂, and n₃. Wave analysis aims to give a prediction for φ₃ in the nonresponse wave. For method one, ${\phi }_3={\phi }_2$. Methods two and three assume a linear relationship for the effect size over time. From Armstrong and Overton (1977)⁵, for method two, φ₃ is calculated as in (16).

Here, a straight line is drawn between the midpoint of group one and the midpoint of group two. The line is extrapolated to the end of group two. For method three, the line is extrapolated to the middle of group three, giving (17).

A wave analysis was performed for each combination of the correlations given in Fig. 5 and the three different nonresponse scenarios. Here, the correlation r is the effect size. The first two wave analysis methods are independent of the number of nonresponses n₃, but the third is not, so the results differ across the three nonresponse scenarios.

The results of the wave analysis are given in Table 7. Results are given for each of the 10 possible correlations between the summated rating scales. The first two columns contain the values of the mean correlation values for waves one and two. The means for the second wave are taken as the M1 (method one) estimate of the third wave. The next column contains the M2 (method two) estimates of the correlations at the end of the second wave and the subsequent columns contain the M3 (method three) estimates for the three levels of participant response (50%, 25%, and 10%). For the moderate response scenarios (50%, 25%), the correlations all stayed within bounds, but for the 10% scenario, several values needed to be truncated at either −1 or 1. This shows the difficulty of a linear interpolation that extends well beyond the range of data. It is likely that as n₃ increases, any change in the dependent variable will lessen. However, the values for 10% response provide useful “extreme bounds”, which can be utilized by the WCRT procedure.

5.4 WCRT Procedure

As previously shown in Fig. 5, all multi-item scale correlations are strongly (p < 0.001) significant, with correlations between scales related to the actual shopping experience (EXP, SAT, POW) over 0.8, correlations between these scales and the future shopping intention (INTENT) scale in the 0.6–0.7 range and the correlations between the general shopping enjoyment measure and the other scales in the 0.2–0.3 range.

For each correlation, the WCRT procedure was calculated for opposing effect sizes with increments of 0.01 ranging from −0.99 to the maximum effect size with a finite n (approximately 0) for alpha (α) values of 0.01, 0.05, and 0.1. Selected results are examined in Figs. 6 and 7 in what we call “n-curves”, which are similar to the n‑curves that have been used to determine sample sizes (e.g., Trafimow, 2018) and the probability of replication (Killeen, 2005), and the previously discussed p‑curves for statistical power (Simonsohn et al., 2014).

Fig. 6 n‑Curve for EXP and SAT: α = 0.05

Fig. 7 n‑Curve for INTENT and ENJOY: α = 0.05

For contrast, curves are given for the highest correlation (EXT and SAT), where r₁ = 0.94, and for the lowest correlation (INTENT and JOY), where r₁ = 0.24. For each of these correlations, curves are given for α = 0.05, though any value of α can be chosen. The x‑axis contains the r₂ required to negate the significance of the significance test⁶. In the case of correlations, due to the asymptotic behavior of the significance test being a tradeoff between the overall effect size and n, only negative r₂ values give a finite n and the graphs go off to infinity at approximately r₂ = 0.

As the relationship between the value of r and n is strongly exponential, it is difficult to plot n versus r on a linear scale, so a logarithmic scale is used for n. This makes it more difficult to read the values of n, but to make up for this, values of n are explicitly given for negatives of the standard effect sizes defined by Cohen (1988), giving r = −0.1 (small), r = −0.3 (medium) and r = −0.5 (large) effect sizes, along with r = −0.7 and r = −0.9.

Looking at Fig. 6, which is for an α = 0.05 test for the pair of scales with the strongest correlation (r₁ = 0.94), for a small negative effect (r₂ = −0.1), n = 5670 would be required to negate significance, while for a large negative effect (r₂ = −0.5), n = 1175 would be required to negate significance. This would be very unlikely, given the large negative effect. Even an almost “complete reversal” of the correlation (r₂ = −0.9) would require n = 454 in order to negate significance.

The graph in Fig. 7 is for an α = 0.05 test for the lowest correlation of r = 0.24 between INTENT and ENJOY, and it shows much lower values of n. For α = 0.05, for a small negative effect (r₂ = −0.1), n = 427 would be required to negate significance, while for a large negative effect (r₂ = −0.5), n = 103 would be required to negate significance. The extreme r₂ = −0.9 case would require n = 43 to negate significance.

5.5 Combining WCRT with Wave Analysis

The combined method was applied to the previously discussed correlation example for all 10 correlations, two significance levels ($\alpha =0.05,0.01)$, and the previously discussed participant nonresponse scenarios (nonresponse n = 415, 1245, 3735). The results are given in Table 8, 9 and 10, with each table containing one of the three nonresponse scenarios. Each table contains a row for each of the ten tested correlations. There are columns for the sample correlation value, the three wave analysis values, and the two WCRT values for the tested values of the Type I error α. As all correlations are significant and positive, the wave analysis results are flagged/counted as reversing the result of the statistical test if the correlations are less than the WCRT values. These flagged correlations are marked with a star (*) symbol.

In Table 8, no values are flagged and none of the wave analysis scenarios will reverse the result of the statistical test. In part, this is because all the test correlations are quite “strong”. Even the correlations that include the ENJOY measure (0.24 ≤ r ≤ 0.27), while less than the other correlations, are strongly significant with a sample size of n = 415. As the nonresponse n₃ increases from 415 to 3735, the magnitude of the correlations found by the inverse WCRT procedure decreases. This is intuitive, as given that statistical significance is a function of both effect size and sample size, for a larger sample size, a smaller negative effect is needed to reverse the results of a statistical test.

In Table 9, the extrapolated r₃ for M3 goes outside of the testing “flip” boundaries defined by WCRT for three correlations, which increases to six correlations for the n₃ = 3735 results given in Table 10. This includes all the “enjoy” correlations except for the “PWOM, ENJOY” correlation, for which there is only a very slight linear trend. Despite negative linear trends, the “EXP, PWOM” and “SAT, PWOM” correlations are not flagged, as the correlations are high relative to the negative linear trends.

6 Discussion

The basic WCRT methodology was developed in this paper as a method for analyzing robustness towards nonresponse bias. However, the methodology is more generally applicable to other scenarios. For any situation where there is a statistical test and some idea of possible “negative effect sizes”, the WCRT methodology can be used to measure robustness. As noted in the introduction, there is a strong push to improve experimental rigor in the behavioral sciences and in marketing. An added urgency was added to this process by reports finding a low level of replicability in behavioral science studies (e.g., Open Science Collaboration, 2015; Stanley et al., 2018) and by high-profile behavioral research scandals and retractions (e.g., Inman et al., 2018; Stricker & Günther, 2019). In addition to the focus on improving statistical rigor described earlier in the paper (e.g., JCR, 2021; Harvey, 2017; Schwab et al., 2011; Wasserstein & Lazar, 2016), there has been a move towards requiring preregistration of experiments (Simmons et al., 2021), i.e., the process of researchers stating the experimental procedure and expected results and storing this information externally in a third-party repository, and to improved sharing and availability of research data (Towse et al., 2021). Including the preregistration information along with a paper submission ensures that the experiment is not altered in an ad-hoc manner to account for unexpected results.

The methods outlined in this paper can easily be incorporated into the behavioral science environment outlined above. Even in a pure experimental setting, some type of nonresponse bias may be present; for example, for a student experiment, a certain number of students in a subject pool could be notified of a study, with only a few participating. When nonresponse bias is not an issue, WCRT can still be used to help examine the robustness of the results. Gelman and Loken (2013) noted that even with preregistration and no p‑hacking, researchers can still bend the rules, for example, choosing the regression technique that gives the best results or choosing whether to use a main effect or interaction effect to justify a hypothesis. Given continued publication bias towards significant results (e.g., Franco et al. 2014; Harrison et al. 2017), there will always be an incentive to choose the research path to give the most significant results, in what statisticians sometimes call “the garden of forking paths”. Rules to increase experimental rigor, such as preregistration, may prune some of these paths, but without being overly restrictive, cannot prevent researchers finding new paths. This is somewhat analogous to the situation of accountants finding new workarounds as rules on tax avoidance are strengthened.

In the context outlined above, WCRT could be utilized as a measure of robustness of results with respect to all possible experimental errors and biases. A range of possible effect sizes for the nonresponse bias could be derived and combined. Feasible nonresponse effect sizes could be derived for nonresponses using wave analysis or using any method for creating feasible bounds (for example, Manski bounds), by collating effect sizes the past literature in the area, or through a meta-analytic p‑curve analysis (Simonsohn et al. 2014). In time, a set of “n” thresholds could be developed to flag results with insufficient robustness to the factors outlined above.

6.1 Limitations and Future Research

This paper develops WCRT methods for hypothesis tests of means, correlations, and simple regression scenarios. To be widely utilized, WCRT methods would need to be developed for a wider range of statistical tests, such as GLM (general linear models) and SEM (structural equation models), as these methods are the most widely used methods in behavioral research. For example, the second Monte Carlo experiment shows how WRCT methods can be utilized to create a heuristic measure of robustness for regression. However, exact statistical inference is limited by the assumptions of the z transform (Fisher, 1921). In meta-analysis regression, multiple groups for different studies are often handled using multi-group fixed-effect or random-effects regression. There is scope to apply these methods (e.g., Borenstein et al. 2010; Hedges & Vevea, 1998) to model WCRT response vs. nonresponse and to create a generalized methodology for WCRT regression analysis.

The scenario outlined above is similar to the scenario that has unfolded in the area of effect size and power calculations, where over time, methods have been developed for a wide range of statistical tests. For the WCRT methods described in this paper to be widely used, it would be important to package them together into a single cohesive software package, in a similar manner to G*Power (Faul et al., 2007), which has become the de-facto standard software package for power analysis.

In the modern internet-mediated environment, more surveys are being conducted using online panels designed to represent certain population characteristics and through co-working/online hiring platforms, such as the Amazon Mechanical Turk (Kees et al., 2017). Determining nonresponse in online environments is difficult, as the survey platform recruitment procedure may be opaque. What exactly constitutes nonresponse in a panel or online working platform? If a set of respondents are notified about an opportunity, then the number of nonresponses can be calculated only if the number notified is reported by the platform. In a co-working platform where respondents search through lists of opportunities, calculating nonresponse may be difficult. If views of an opportunity are recorded (e.g., through a scroll-down list), then some measure of nonresponse of “aware” respondents can be calculated, but determining how to set a threshold for awareness would be difficult. There has been some initial work on analyzing nonresponse for the Mechanical Turk for longitudinal studies (Daly & Nataraajan, 2015) and several studies have tried to quantify possible nonresponse bias for online platforms (Boas et al., 2020; Paolacci et al., 2010). However, there is strong scope for a systematic analysis of nonresponse for online surveys. Such analysis could include work from both information systems and experimental standpoints, and could include aspects such as data reporting, human-computer interaction, and nonresponse behavior.

The wave analysis method utilized in this paper is a simple linear extrapolation method. Linear extrapolation may not be reliable outside of the range of the data. It is likely that significant linear trends would probably “damp” outside of the range of the data, particularly in situations where there are many nonrespondents. This is a reason why damped trend forecasting methods that give conservative forecasts are often successful (e.g., Armstrong et al., 2015; Gardner, 2015). For the use of wave analysis in the experimental section, this lack of conservatism is an advantage, as linear extrapolation is used to create worst case bounds for correlations. However, given the advances in forecasting over the 40 plus years since the introduction of wave analysis (e.g., Makridakis et al., 2020), there is scope to bring new methodology to bear on wave analysis and develop methods to improve forecasts of nonresponse bias.

1 Supplementary Information

Open Practices Statement

The dataset collated for this paper and the code for the procedures developed in the paper have made available at https://github.com/MDSOPT/WCRT.

References

Aiken, L. R. (1981). Proportion of returns in survey research. Educational and Psychological Measurement, 41(4), 1033–1038. a, b

Akkucuk, U., & Carroll, J. D. (2006). PARAMAP vs. Isomap: a comparison of two nonlinear mapping algorithms. Journal of Classification, 23, 221–254. →

Armstrong, J. S., & Overton, T. S. (1977). Estimating nonresponse bias in mail surveys. Journal of Marketing Research, 14(3), 396–402. a, b, c, d, e, f, g

Armstrong, J. S., Green, K. C., & Graefe, A. (2015). Golden rule of forecasting: be conservative. Journal of Business Research, 68(8), 1717–1731. →

Babić Rosario, A., Sotgiu, F., De Valck, K., & Bijmolt, T. H. (2016). The effect of electronic word of mouth on sales: a meta-analytic review of platform, product, and metric factors. Journal of Marketing Research, 53(3), 297–318. →

Banfield, J. D., & Raftery, A. E. (1993). Model-based Gaussian and non-Gaussian clustering. Biometrics, 49(3), 803–821. →

Baroudi, J. J., & Orlikowski, W. J. (1989). The problem of statistical power in MIS research. MIS Quarterly, 13(1), 87–106. a, b

Beebe, T. J., Talley, N. J., Camilleri, M., Jenkins, S. M., Anderson, K. J., & Locke III, G. R. (2011). Health insurance portability and accountability act (HIPAA) authorization and survey nonresponse bias. Medical Care, 49(4), 365–370. →

Berg, N. (2005). Non-response bias. In K. Kempf-Leonard (Ed.), Encyclopedia of social measurement (Vol. 2, pp. 865–873). Academic Press. →

Bland, J. M., & Altman, D. G. (1997). Statistics notes: Cronbach’s alpha. BMJ, 314(7080), 572. →

Boas, T. C., Christenson, D. P., & Glick, D. M. (2020). Recruiting large online samples in the United States and India: Facebook, Mechanical Turk, and Qualtrics. Political Science Research and Methods, 8(2), 232–250. a, b

Borenstein, M., Hedges, L. V., Higgins, J. P., & Rothstein, H. R. (2010). A basic introduction to fixed-effect and random-effects models for meta-analysis. Research Synthesis Methods, 1(2), 97–111. →

Boyd Jr., H. W., & Westfall, R. (1965). Interviewer bias revisited. Journal of Marketing Research, 2(1), 58–63. →

Brusco, M. J., Singh, R., Cradit, J. D., & Steinley, D. (2017). Cluster analysis in empirical OM research: survey and recommendations. International Journal of Operations & Production Management, 37(3), 300–320. →

Cashen, L. H., & Geiger, S. W. (2004). Statistical power and the testing of null hypotheses: a review of contemporary management research and recommendations for future studies. Organizational Research Methods, 7(2), 151–167. a, b

Chandler, J., Rosenzweig, C., Moss, A. J., Robinson, J., & Litman, L. (2019). Online panels in social science research: expanding sampling methods beyond Mechanical Turk. Behavior Research Methods, 51(5), 2022–2038. →

Chen, L., & Buja, A. (2009). Local multidimensional scaling for nonlinear dimension reduction, graph drawing, and proximity analysis. Journal of the American Statistical Association, 104(485), 209–219. →

Chesney, D. L., & Obrecht, N. A. (2012). Statistical judgments are influenced by the implied likelihood that samples represent the same population. Memory & Cognition, 40(3), 420–433. →

Coe, R. (2002). It’s the effect size, stupid: what effect size is and why it is important. In Annual Conference of the British Educational Research Association (pp. 1–18). British Educational Research Association. →

Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd edn.). Lawrence Erlbaum. a, b, c, d

Cohen, J. (1992). A power primer. Psychological Bulletin, 112(1), 155–159. a, b

Collier, J. E., & Bienstock, C. C. (2007). An analysis of how nonresponse error is assessed in academic marketing research. Marketing Theory, 7(2), 163–183. →

Cook, C., Heath, F., & Thompson, R. L. (2000). A meta-analysis of response rates in web-or internet-based surveys. Educational and Psychological Measurement, 60(6), 821–836. →

Cox, N. J. (2008). Speaking Stata: Correlation with confidence, or Fisher’s z revisited. The Stata Journal, 8(3), 413–439. →

Cronbach, L. J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika, 16(3), 297–334. →

Daikeler, J., Bošnjak, M., & Lozar Manfreda, K. (2020). Web versus other survey modes: an updated and extended meta-analysis comparing response rates. Journal of Survey Statistics and Methodology, 8(3), 513–539. →

Daly, T. M., & Nataraajan, R. (2015). Swapping bricks for clicks: crowdsourcing longitudinal data on Amazon turk. Journal of Business Research, 68(12), 2603–2609. →

Daniel, W. W., Schott, B., Atkins, F. C., & Davis, A. (1982). An adjustment for nonresponse in sample surveys. Educational and Psychological Measurement, 42(1), 57–67. →

Deming, W. E. (1953). On a probability mechanism to attain an economic balance between the resultant error of response and the bias of nonresponse. Journal of the American Statistical Association, 48(264), 743–772. →

Diamantopoulos, A., & Winklhofer, H. M. (2001). Index construction with formative indicators: an alternative to scale development. Journal of Marketing Research, 38(2), 269–277. →

Faul, F., Erdfelder, E., Lang, A. G., & Buchner, A. (2007). G* Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behavior Research Methods, 39(2), 175–191. a, b

Field, A. P. (2001). Meta-analysis of correlation coefficients: A Monte Carlo comparison of fixed- and random-effects methods. Psychological Methods, 6(2), 161–180. →

Fisher, R. A. (1921). On the “probable error” of a coefficient of correlation deduced from a small sample. Metron, 1, 13–32. a, b, c

France, S. L., Adams, F. G., & Landers, V. M. (2024a). Dataset for worst case resistance testing: a nonresponse bias solution for today’s survey research realities. Ann Arbor: Inter-university Consortium for Political and Social Research [distributor]. https://doi.org/10.3886/E203261V2. →

France, S. L., Adams, F., & Landers, M. (2024b). Software for worst case resistance testing: nonresponse bias solution for today’s survey research realities. https://github.com/MDSOPT/WCRT  

Franco, A., Malhotra, N., & Simonovits, G. (2014). Publication bias in the social sciences: unlocking the file drawer. Science, 345(6203), 1502–1505. →

Gardner, E. S. (2015). Conservative forecasting with the damped trend. Journal of Business Research, 68(8), 1739–1741. →

Gelman, A., & Loken, E. (2013). The garden of forking paths: Why multiple comparisons can be a problem, even when there is no “fishing expedition” or “p-hacking” and the research hypothesis was posited ahead of time. https://stat.columbia.edu/~gelman/research/unpublished/forking.pdf  →

Gill, J. (1999). The insignificance of null hypothesis significance testing. Political Research Quarterly, 52(3), 647–674. →

Groves, R. M. (2006). Nonresponse rates and nonresponse bias in household surveys. Public Opinion Quarterly, 70(5), 646–675. a, b

Groves, R. M., & Peytcheva, E. (2008). The impact of nonresponse rates on nonresponse bias: a meta-analysis. Public Opinion Quarterly, 72(2), 167–189. →

Halbesleben, J. R. B., & Whitman, M. V. (2013). Evaluating survey quality in health services research: a decision framework for assessing nonresponse bias. Health Services Research, 48(3), 913–930. →

Harrison, J. S., Banks, G. C., Pollack, J. M., O’Boyle, E. H., & Short, J. (2017). Publication bias in strategic management research. Journal of Management, 43(2), 400–425. →

Hartman, B. W., Fuqua, D. R., & Jenkins, S. J. (1986). The problems of and remedies for nonresponse bias in educational surveys. The Journal of Experimental Education, 54(2), 85–90. →

Harvey, C. R. (2017). Presidential address: the scientific outlook in financial economics. The Journal of Finance, 72(4), 1399–1440. a, b

Hedges, L. V., & Vevea, J. L. (1998). Fixed- and random-effects models in meta-analysis. Psychological Methods, 3(4), 486. a, b

Hemphill, J. F. (2003). Interpreting the magnitudes of correlation coefficients. American Psychologist, 58(1), 78–79. →

Hernán, M. A., & Robins, J. M. (2020). Causal inference. Chapman & Hall/CRC. https://www.hsph.harvard.edu/miguel-hernan/causal-inference-book/  →

Higgins, J. P., Thomas, J., Chandler, J., Cumpston, M., Li, T., Page, M. J., & Welch, V. A. (Eds.). (2019). Cochrane handbook for systematic reviews of interventions. John Wiley & Sons. a, b

Horowitz, J. L., & Manski, C. F. (1998). Censoring of outcomes and regressors due to survey nonresponse: identification and estimation using weights and imputations. Journal of Econometrics, 84(1), 37–58. a, b

Hubbard, R., & Armstrong, J. S. (2006). Why we don’t really know what statistical significance means: implications for educators. Journal of Marketing Education, 28(2), 114–120. →

Hunter, J. E. (1997). Needed: a ban on the significance test. Psychological Science, 8(1), 3–7. →

Inman, J. J., Campbell, M. C., Kirmani, A., & Price, L. L. (2018). Our vision for the Journal of Consumer Research: it’s all about the consumer. Journal of Consumer Research, 44(5), 955–959. a, b

JCR (2021). Journal of Consumer Research: Research Ethics. https://consumerresearcher.com/research-ethics. Accessed 02.06. a, b

Kanuk, L., & Berenson, C. (1975). Mail surveys and response rates: a literature review. Journal of Marketing Research, 12(4), 440–453. a, b

Kees, J., Berry, C., Burton, S., & Sheehan, K. (2017). An analysis of data quality: professional panels, student subject pools, and Amazon’s Mechanical Turk. Journal of Advertising, 46(1), 141–155. →

Kelley, K., & Preacher, K. J. (2012). On effect size. Psychological Methods, 17(2), 137–152. →

Killeen, P. R. (2005). An alternative to null-hypothesis significance tests. Psychological Science, 16(5), 345–353. →

Lambert, D. M., & Harrington, T. C. (1990). Measuring nonresponse bias in customer service mail surveys. Journal of Business Logistics, 11(2), 5–25. →

Lee, S. (2006). Propensity score adjustment as a weighting scheme for volunteer panel web surveys. Journal of Official Statistics, 22(2), 329. a, b

Leventhal, L., & Huynh, C. L. (1996). Directional decisions for two-tailed tests: Power, error rates, and sample size. Psychological Methods, 1(3), 278. →

MacDonald, S. E., Newburn-Cook, C. V., Schopflocher, D., & Richter, S. (2009). Addressing nonresponse bias in postal surveys. Public Health Nursing, 26(1), 95–105. →

Makridakis, S., Hyndman, R. J., & Petropoulos, F. (2020). Forecasting in social settings: the state of the art. International Journal of Forecasting, 36(1), 15–28. →

Manski, C. F. (2016). Credible interval estimates for official statistics with survey nonresponse. Journal of Econometrics, 191(2), 293–301. a, b

Mende, M., Scott, M. L., van Doorn, J., Grewal, D., & Shanks, I. (2019). Service robots rising: how humanoid robots influence service experiences and elicit compensatory consumer responses. Journal of Marketing Research, 56(4), 535–556. →

Milligan, G. W. (1981). A Monte Carlo study of thirty internal criterion measures for cluster analysis. Psychometrika, 46, 187–199. →

Mohr, J., & Spekman, R. (1994). Characteristics of partnership success: partnership attributes, communication behavior, and conflict resolution techniques. Strategic Management Journal, 15(2), 135–152. →

Newman, D. A. (2009). Missing data techniques and low response rates. In I. C. E. Lance & R. J. Vandenberg (Eds.), Statistical and methodological myths and Urban legends: doctrine, verity and fable in the organizational and social sciences (pp. 7–36). Routledge. a, b

Olson, K. (2006). Survey participation, nonresponse bias, measurement error bias, and total bias. Public Opinion Quarterly, 70(5), 737–758. →

Open Science Collaboration (2015). Estimating the reproducibility of psychological science. Science, 349(6251), aac4716-1–aac4716‑8. →

Paolacci, G., Chandler, J., & Ipeirotis, P. G. (2010). Running experiments on Amazon Mechanical Turk. Judgment and Decision Making, 5(5), 411–419. a, b

Pavlou, P. A. (2003). Consumer acceptance of electronic commerce: integrating trust and risk with the technology acceptance model. International Journal of Electronic Commerce, 7(3), 101–134. →

Peer, E., Brandimarte, L., Samat, S., & Acquisti, A. (2017). Beyond the Turk: alternative platforms for crowdsourcing behavioral research. Journal of Experimental Social Psychology, 70, 153–163. →

Qualtrics (2020). Online samples. https://www.qualtrics.com/research-services/online-sample/. Accessed 04.12. →

Rogelberg, S. G., & Stanton, J. M. (2007). Introduction: understanding and dealing with organizational survey nonresponse. Organizational Research Methods, 10(2), 195–209. a, b, c, d

Rogelberg, S. G., Luong, A., Sederburg, M. E., & Cristol, D. S. (2000). Employee attitude surveys: examining the attitudes of noncompliant employees. Journal of Applied Psychology, 85(2), 284–293. →

Rogelberg, S. G., Conway, J. M., Sederburg, M. E., Spitzmüller, C., Aziz, S., & Knight, W. E. (2003). Profiling active and passive nonrespondents to an organizational survey. Journal of Applied Psychology, 88(6), 1104. →

Rosenberg, M. S. (2005). The file-drawer problem revisited: a general weighted method for calculating fail-safe numbers in meta-analysis. Evolution, 59(2), 464–468. a, b

Rosenthal, R. (1979). The file drawer problem and tolerance for null results. Psychological Bulletin, 86(3), 638–641. a, b

Rosenthal, R., & Rubin, D. B. (1982). Comparing effect sizes of independent studies. Psychological Bulletin, 92(2), 500–504. →

Roth, P. L. (1994). Missing data: a conceptual review for applied psychologists. Personnel Psychology, 47(3), 537–560. →

Rotnitzky, A., Robins, J. M., & Scharfstein, D. O. (1998). Semiparametric regression for repeated outcomes with nonignorable nonresponse. Journal of the American Statistical Association, 93(444), 1321–1339. a, b

Sawyer, A. G., & Ball, A. D. (1981). Statistical power and effect size in marketing research. Journal of Marketing Research, 18(3), 275–290. →

Scharfstein, D. O., & Irizarry, R. A. (2003). Generalized additive selection models for the analysis of studies with potentially nonignorable missing outcome data. Biometrics, 59(3), 601–613. a, b

Schneider, J. W. (2015). Null hypothesis significance tests. A mix-up of two different theories: the basis for widespread confusion and numerous misinterpretations. Scientometrics, 102(1), 411–432. →

Schonlau, M., Van Soest, A., Kapteyn, A., & Couper, M. (2009). Selection bias in web surveys and the use of propensity scores. Sociological Methods & Research, 37(3), 291–318. a, b

Schwab, A., Abrahamson, E., Starbuck, W. H., & Fidler, F. (2011). Researchers should make thoughtful assessments instead of null-hypothesis significance tests. Organization Science, 22(4), 1105–1120. a, b

Sevilla, J., & Townsend, C. (2016). The space-to-product ratio effect: How interstitial space influences product aesthetic appeal, store perceptions, and product preference. Journal of Marketing Research, 53(5), 665–681. →

Simmons, J. P., Nelson, L. D., & Simonsohn, U. (2011). False-positive psychology: undisclosed flexibility in data collection and analysis allows presenting anything as significant. Psychological Science, 22(11), 1359–1366. →

Simmons, J. P., Nelson, L. D., & Simonsohn, U. (2021). Pre-registration: why and how. Journal of Consumer Psychology, 31(1), 151–162. →

Simonsohn, U., Nelson, L. D., & Simmons, J. P. (2014). P‑curve: a key to the file-drawer. Journal of Experimental Psychology: General, 143(2), 534. a, b, c

Sirdeshmukh, D., Singh, J., & Sabol, B. (2002). Consumer trust, value, and loyalty in relational exchanges. Journal of Marketing, 66(1), 15–37. →

Sitter, R. R. (1992). Comparing three bootstrap methods for survey data. Canadian Journal of Statistics, 20(2), 135–154. →

Skafida, V., Morrison, F., & Devaney, J. (2022). Answer refused: exploring how item non-response on domestic abuse questions in a social survey affects analysis. Survey Research Methods, 16(2), 227–240. →

Sosdian, C. P., & Sharp, L. M. (1980). Nonresponse in mail surveys: access failure or respondent resistance. The Public Opinion Quarterly, 44(3), 396–402. →

Stanley, T. D., Carter, E. C., & Doucouliagos, H. (2018). What meta-analyses reveal about the replicability of psychological research. Psychological Bulletin, 144(12), 1325–1346. a, b

Stricker, J., & Günther, A. (2019). Scientific misconduct in psychology. Zeitschrift Für Psychologie, 227(1), 53–63. →

Szymanski, D. M., & Henard, D. H. (2001). Customer satisfaction: a meta-analysis of the empirical evidence. Journal of the Academy of Marketing Science, 29(1), 16–35. →

Tavakol, M., & Dennick, R. (2011). Making sense of Cronbach’s alpha. International Journal of Medical Education, 2, 53–55. →

Towse, J. N., Ellis, D. A., & Towse, A. S. (2021). Opening Pandora’s Box: peeking inside Psychology’s data sharing practices, and seven recommendations for change. Behavior Research Methods, 53(4), 1455–1468. →

Trafimow, D. (2017). Why it is problematic to calculate probabilities of findings given range null hypotheses. Open Journal of Statistics, 7(3), 483–499. →

Trafimow, D. (2018). Confidence intervals, precision and confounding. New Ideas in Psychology, 50, 48–53. a, b

Valentine, K. D., Buchanan, E. M., Scofield, J. E., & Beauchamp, M. T. (2019). Beyond p values: utilizing multiple methods to evaluate evidence. Behaviormetrika, 46, 121–144. →

Wasserstein, R. L., & Lazar, N. A. (2016). The ASA statement on p‑values: context, process, and purpose. The American Statistician, 70(2), 129–133. a, b

Wetzel, M., & Hünteler, B. (2022). The blind spot: studying the association between survey nonresponse and adherence to COVID-19 governmental regulations in a population-based German web-survey. Survey Research Methods, 16(3), 267–281. a, b

Woolston, C. (2015). Psychology journal bans P values. Nature News, 519(7541), 9–9. →