The Performance of Multiple Imputation in Social Surveys with Missing Data from Planned Missingness and Item Nonresponse

1 Introduction

Survey designs using planned missingness are recently receiving a lot of attention in social survey research. This is marked by a growing body of research, particularly focusing on how to design the planned missingness patterns in such surveys (e.g., Adigüzel and Wedel 2008; Axenfeld et al. 2022a; Bahrami et al. 2014; Imbriano and Raghunathan 2020; Thomas et al. 2006). Increasingly, designs with planned missingness are also being applied in large-scale social surveys, such as the European Values Study 2017 (Luijkx et al. 2021) or the PISA 2012 context questionnaire (OECD 2014:48–58). Examples of planned missingness designs are multiple matrix sampling (Shoemaker 1973; Munger and Loyd 1988), two-method measurement designs (Graham et al. 2006), and the X‑form design (Graham et al. 1996) or (similarly) the split questionnaire design (SQD; Raghunathan and Grizzle 1995).

The SQD entails leaving out items for each respondent based on a random procedure. This usually serves to shorten questionnaires for individual respondents, considering that lengthy questionnaires can lead to reduced response rates, high breakoff, and increased measurement error (Galesic and Bosnjak 2009; Peytchev and Peytcheva 2017). This especially applies to self-administered online surveys (Callegaro et al. 2015; de Leeuw 2008), which increasingly tend to compete with traditional face-to-face surveys.

The resulting planned missing data (PMD) is usually considered missing completely at random (MCAR). Yet, as all cases and most variables would be incomplete, simple pairwise deletion may often result in insufficient net sample sizes. Thus, as proposed by Raghunathan and Grizzle (1995), missing data from SQDs may need to be imputed.

Meanwhile, additional sources of missing data are typically present as well in SQD surveys. In particular, item nonresponse (INR) by survey participants is a common issue.¹ Unlike unit nonresponse, INR has been found to be little responsive to variations in survey length (Galesic and Bosnjak 2009). Thus, we may expect that INR constitutes a similar challenge to SQD and conventional surveys alike. This also includes the potential for nonresponse bias, which would require appropriate treatment (see, for example, Durrant 2009; Frick and Grabka 2005; Rässler and Riphahn 2006) through statistical techniques such as multiple imputation (MI; Rubin 1987; van Buuren 2018). Yet, INR is often not considered explicitly in research on imputing SQD survey data.

A realistic scenario of imputing SQD survey data has to take different types of missingness into account: PMD by the design and INR by the participants. These two types of missingness combined may cause an adverse scenario for the imputation: First, both types of missingness may in combination sum up to a very large overall proportion of missing data. On the one hand, this is because a considerable reduction in questionnaire length requires an equivalent amount of PMD. On the other hand, INR can unexpectedly cause considerable amounts of missingness because participants’ response behaviour is not under the control of the survey designer. Second, INR by participants may occur non-randomly, potentially causing nonresponse bias. In consequence, imputation models need to account for a potentially heterogeneous, non-random missingness mechanism for a potentially very large amount of missing data. This is important also because the resulting low case numbers available for the imputation model might hamper its capacity to account for the variables relevant for the response mechanism. Consequently, both types of missingness combined in a survey might adversely affect estimates after imputing the data. All this implies that future implementations of SQDs in social surveys may depend crucially on appropriate research telling if and under which conditions accurate estimates can be obtained. Existing research on imputing SQD survey data does not provide such inference.

We contribute to this research gap by investigating how the simultaneous occurrence of PMD and INR in social surveys affects estimates after imputation. In doing so, we seek to determine to what extent SQDs might still constitute a useful tool for social surveys when additional INR is factored in. We also examine if the imputation is able to deal with bias introduced by INR in such a situation.

In this paper, we use a Monte Carlo simulation study based on real social survey data. We vary the proportion of PMD, the proportion of INR, and the mechanism producing the INR. We investigate the accuracy of univariate frequency and bivariate correlation estimates after imputation in the different scenarios.

2 Theory

2.1 Missingness mechanisms

Missing data can have different effects on the analysis of survey data depending on the missingness mechanism. There are three types of missingness mechanisms (Rubin 1976; Little and Rubin 2020): missing completely at random (MCAR), missing at random (MAR), and missing not at random (MNAR).

In the MCAR condition all observations have the same probability of being missing independent of any observed or relevant unobserved data. Consequently, the missingness does not introduce bias to analyses of the data. Hence, such data can in principle be analysed using only the complete cases. However, this strategy may yield small case numbers if there is a relevant share of missing data. Thus, MCAR may not directly introduce bias, but it can pose challenges through the consequential loss of cases for the analysis. This may result in larger standard errors or potentially even render the estimation unfeasible due to insufficient pairwise observations.

If the missing data are MAR, the missingness Z may depend on any observed data

but not on the missing data

. In this situation, dropping incomplete cases from the analysis may result in biased estimates. Yet, we may still obtain unbiased and approximately efficient estimates through appropriate methods such as MI (Rubin 1987), which model the missingness mechanism for

based on the information in the other variables,

.

Under MNAR, by contrast, Z depends on the missing data

itself or other unobserved parameters even after conditioning on

. This applies especially if the missing data in a variable j depends on

, i.e., the concerned variable itself. In this situation, conventional imputation procedures relying only on conditioning on

are invalid (van Buuren 2018). It obviously is not possible to condition on

either, since this information is missing. This can be resolved through specialized MNAR imputation procedures that introduce external information on the selection into

to the imputation model. For instance, imputed values can be shifted upwards or downwards to match a known distribution (pattern-mixture models; Glynn et al. 1986) or prespecified response weights can be used (selection models; Heckman 1976; for a detailed discussion of both methods, see Little 2009). Another approach by Carpenter et al. (2007) proposes weighting the multiple estimates for a parameter produced by MI in order to correct for a MNAR mechanism. However, for social survey data such external information is often not available. Therefore, research practice often relies on more pragmatic approaches. When the MAR assumption is questionable, it is often suggested to use imputation procedures for MAR mechanisms but include as much information predictive of the missingness as possible into the imputation model to reduce bias in estimates (Collins et al. 2001; van Buuren 2018, p. 165). Consequently, our study assumes that no external information on the missing data is available.

2.2 Planned missing data (PMD)

SQDs may yield large amounts of missing data for each respondent and on all variables excluding the core. This is because a meaningful reduction in questionnaire length presupposes a large amount of questions remaining unasked: Reducing the number of items presented to each respondent by 50%, for example, requires overall 50% PMD. This also leaves all cases and all split-module variables incompletely observed. As a result, analysis strategies relying only on the complete cases may end up with an insufficient number of cases or no cases at all. In consequence, Raghunathan and Grizzle (1995) propose imputing PMD to obtain analysable data from SQDs.

2.3 Item nonresponse (INR)

There can be various reasons for INR: Respondents may not understand the question, not know or be sure about the correct response, lack motivation to form an opinion, forget to respond, refuse to answer a sensitive question, or their response may get lost due to an error during data collection or processing (Bech and Kristensen 2009; Berinsky 2008; de Leeuw et al. 2003; Montagni et al. 2019; Shoemaker et al. 2002). Correspondingly, various missingness mechanisms generating INR are worth considering.

MCAR is a particularly strong assumption which may be realistic for INR only in specific exceptions. For example, data losses at coding or data processing could result in MCAR. Usually, however, social survey research considers the MCAR assumption untenable (de Leeuw et al. 2003; Durrant 2009).

MAR often appears as a more realistic assumption since it allows the INR to depend on respondent characteristics: INR generally occurs more often among respondents that are older (Bech and Kristensen 2009; Blumenberg et al. 2018; Callens and Loosveldt 2018; Elliott et al. 2005; Klein et al. 2011; Meitinger and Johnson 2020; Messer et al. 2012), less educated (Blumenberg et al. 2018; Callens and Loosveldt 2018; Meitinger and Johnson 2020; Messer et al. 2012), belong to a (particularly ethnic) minority group (Elliott et al. 2005; Klein et al. 2011; Meitinger and Johnson 2020) or are not that interested in the survey topic (Callens and Loosveldt 2018; Kmetty and Stefkovics 2021). INR rates can also differ considerably between geographic regions (Callens and Loosveldt 2018; Bech and Kristensen 2009). Yet, the role of respondent characteristics for INR often varies between different questions and surveys: Some surveys report higher INR among women than men (Bech and Kristensen 2009; Callens and Loosveldt 2018; Elliott et al. 2005; Klein et al. 2011; Meitinger and Johnson 2020; Washington Community Survey, see Messer et al. 2012), while others experience no differences (Lewiston and Clarkston Quality of Life Survey and Washington Economic Survey, see Messer et al. 2012). Some surveys show a negative association between income and INR (Klein et al. 2011), while others show no clear association, especially in online surveys (Messer et al. 2012). There may be additional, potentially unknown variables that are associated with the INR on a variable. However, the MAR assumption is reasonable only if one is confident that all variables relevant for the nonresponse mechanism are available in the observed data.

INR can also result from a MNAR mechanism. This may occur when respondents deem their potential answer sensitive or socially undesirable (Copas and Farewell 1998; de Leeuw et al. 2003; Rässler and Riphahn 2006; Tourangeau and Yan 2007). For example, respondents with high income tend to refuse reporting their income (see, for example, Rässler and Riphahn 2006; Yan et al. 2010).

2.4 Imputation

MI (Rubin 1987; van Buuren 2018) is one of the current state-of-the-art procedures for imputation. It aims to both preserve relations in the data and ensure variability. To impute univariate missing data in a variable j using MI, for each missing value a number of m (multiple) imputations are drawn based on an imputation model. This imputation model estimates the distribution of

conditional on other variables in

using a pre-specified imputation method. Drawing m imputations from the conditional distribution yields m imputed datasets and m varying imputed values for each missing value. These multiple datasets are then analysed separately and the resulting estimates pooled into combined estimates according to Rubin’s rules (Rubin 1987; see also van Buuren 2018:145–147).

For multivariate missing data, a common solution is MI by fully conditional specification (FCS; van Buuren et al. 2006). This approach relies on looping through different imputation models that impute missing data in each variable separately. For each variable to be imputed, this involves specifying an imputation method and the relevant predictor variables.

The general procedure of FCS is as follows: We initially replace all missing values by starting values randomly drawn from the marginal distributions of the variables to be imputed. Then we impute the first variable,

, based on the observed data and initial starting values of the predictor variables, replacing the initial starting values in

by the new imputed ones. We proceed by imputing

using the observed and imputed values in

(provided that

is in the predictor set) and the observed and initial starting values in the remaining predictor variables, replacing the initial starting values in

by new imputed ones. This continues until all variables in X are imputed. Subsequently, we repeat this procedure with the previously imputed values instead of the initial starting values: Again, we begin with imputing

,

up to

and steadily replace the old imputations by new ones. This looping procedure is repeated for a small (prespecified) number of iterations for convergence, after which the final imputations are drawn. To create m multiple imputations, this entire procedure is repeated m times.

When both PMD and INR appear in a survey, the imputation task might be affected adversely. As described above, SQD surveys tend to generate PMD already on a large scale. In practice, this could lead to enormous proportions of missing data in total, since the amount of INR is not under the researchers’ deliberate control. This is important because it means the imputation model may need to rely on little observed data. Especially for the imputation of INR this is far from ideal since we would prefer to have as much information on the missing data and its mechanism as possible. Furthermore, more missing data also means a larger impact of imputed values on the estimation, suggesting greater potential for bias from a poor imputation model.

As noted above, an additional challenge may be that PMD and INR may stem from different missingness mechanisms (MCAR and potentially not MCAR). In this context, one might want to account for the different nature of both types of missingness. This would mean to impute a variable j conditional on

or

(for example, by imputing both types of missingness separately). However, in our view this is not meaningful. First, separate imputation models for INR and PMD would likely have to rely on the same observed data

that neither experienced planned missingness nor INR, as we only have observations on x_i,j when

. Moreover, being affected by INR (

), the remaining available data

may not be subject to a randomness comparable to the PMD anymore without conditioning on the variables determining the INR. Thus, an attempt to impute

separate from

cannot legitimately be considered MCAR. Finally, even if these challenges were overcome, imputation models conditioning on

or

would likely imply considerably more model parameters to be estimated or (in case of separate models) considerably smaller case numbers. This might be difficult considering we have limited case numbers available but potentially many predictor variables to consider. Therefore, for each variable to be imputed we build one imputation model imputing all missing values together based on Z without conditioning on Z^ψ or Z^ω.

Thus, we may face a complex missing-data problem with (a) potentially very large proportions of missing data and (b) a potentially complex, heterogeneous missingness mechanism. This complicated missingness mechanism needs to be represented in one single imputation model per variable. This model needs to include all variables predicting the INR despite a potential lack of available cases to support such an extensive model. Thus, the question is how well the imputation can reproduce relevant data structures in spite of these challenges.

3 Data and Method

To examine the impact of INR and PMD on estimates after imputation, we apply a Monte Carlo (MC) simulation study using real social survey data.² To allow for a realistic simulation of INR, we first investigate how frequently INR occurs and identify its determinants in the survey dataset that subsequently serves as population data for the simulation study. In each simulation run we draw a random sample from this population dataset and use the information from the preliminary analysis to simulate INR using a procedure similar to Enderle et al. (2013). We also simulate PMD from an SQD with random modules (see Axenfeld et al. 2022a). Thus, each simulation run involves stochastically generating both PMD and INR. Through this repeated procedure, we can measure robustly to what extent estimates from our data would be MC biased depending on different PMD and INR scenarios.

3.1 Data

The population dataset for this study stems from the German Internet Panel (GIP; Blom, Gathmann and Krieger 2015; Cornesse et al. 2022), an online panel survey of the German general population. We use items from waves 37 and 38 (Blom et al. 2019a, b) primarily on sociodemographic characteristics, political opinions, organization membership and the Big-Five personality traits. Thereby, we obtain a dataset with 61 variables (see also Axenfeld et al. 2022a, b) that are all categorical, mostly ordinal or binary.³

In the MC study, all missing data need to be simulated stochastically. Thus, we need an initially fully observed dataset. To this end, we exclude all unit nonrespondents from the data, reducing the number of cases to 4061. Furthermore, we complement some further missing values with data from waves 1 and 13 (Blom et al. 2016a, b). Finally, we impute the remaining INR using stochastic single imputation by predictive mean matching, a procedure preserving the variance and relationships in the imputed data (Little and Rubin 2020, pp. 76–80).

Beyond that, we combine rare events in variables (i.e., categories with

cases) into broader categories. This is necessary because in some scenarios, observed case numbers in each simulation run correspond to only 16% of the numbers in the population.

3.2 MC simulation procedure

3.2.1 Simulating PMD

3.2.2 Simulating INR

We simulate INR based on the real INR in the GIP. A preliminary analysis shows that overall, 5% of the GIP data are missing due to INR (excluding the sociodemographic items, which are almost completely observed). INR propensities vary heavily by item, ranging from 1 to 19%. Furthermore, to determine how INR propensities vary by survey participant, we estimate elastic-net logistic regression models (Zou and Hastie 2005) of the variables’ INR indicators on all other variables in the dataset. This provides us with estimated nonresponse propensities specific for each observation in the population data. More detailed information on the preliminary analysis can be found in Appendix A.

These nonresponse propensities are used for simulating INR: We draw values from a uniform distribution U(0;1) and set a value missing if its nonresponse propensity is larger than the value drawn from U(0;1) (see Enderle et al. 2013).

We implement four scenarios with different proportions of INR: one with INR approximately as frequent as in the GIP (overall proportion of INR in the split modules: 5%), and three with INR two times (10%), three times (15%), or four times (20%) as frequent as in the GIP. The sociodemographic core module and further six variables in the split modules remain completely observed, as they show no noteworthy INR. As in the real data, the proportions of INR vary considerably by variable with a minimum of 0% and a maximum of 19% (considering the scenario with overall 5% INR).

Hence, the total proportion of missing data in the simulation study depends on the combination of INR and PMD. To illustrate this, Table 1 depicts the combined overall proportion of missing data from both simulation steps for the various scenarios. Accordingly, our simulation scenarios cover overall proportions of missing data ranging from 0 to 68%. This table again highlights why INR and PMD cannot clearly be separated in the imputation: 60% PMD and 20% INR, for instance, do not result in 80 but 68% missing data. Hence, there is a 12% overlap of observations that would be missing both by design and nonresponse.

We also implement different potential nonresponse mechanisms (MCAR, MAR, and MNAR) through adapting the nonresponse propensities.

Under MCAR, INR occurs purely by random chance. Thus, each variable j has nonresponse propensities equal to the proportion of INR on variable j (not varying between respondents). For larger proportions of INR, the propensities are multiplied by 2, 3, or 4. In principle, this procedure can lead to nonresponse propensities larger than 1. However, since all variables in the GIP dataset have proportions of INR smaller than 25%, this is not the case here.

Under MAR, the nonresponse in a variable j depends on data in other variables in

. Thus, for a MAR scenario with INR as frequent as in the GIP, we use the nonresponse propensities estimated in the preliminary analysis using logistic regression models. For the scenarios with more INR, we manipulate the intercepts of these models increasing them such that the resulting propensities turn out two, three, or four times larger on average.

Yet, the MAR mechanism in our data might be too modest to differ substantially from an MCAR scenario. This is why we also consider an amplified MAR mechanism. In these scenarios, we multiply the regression coefficients of the logistic models by 2 and subsequently adjust the intercepts such that the proportion of INR on each variable remains the same as in the GIP-like MAR scenarios.

Under MNAR, we assume that INR on variable j depends only on variable j itself. For this, we set up the following MNAR model

where

is the intercept and

is the regression coefficient of

determining the INR in a variable j. In doing so,

and

are specified so that the mean and the standard deviation of the nonresponse propensities are approximately the same as under the (GIP-like) MAR scenario. For the scenarios with more INR, the intercept

is adjusted as described in the MAR scenario.

In consequence, we end up with

simulation scenarios:

• four scenarios with varying prevalence of PMD (0, 20, 40, 60% PMD) without INR, plus

• four scenarios with varying prevalence of INR (5, 10, 15, 20%), times

• four missingness mechanisms for INR (MCAR, GIP-like MAR, amplified MAR, MNAR), times

• four scenarios with varying prevalence of PMD (0, 20, 40, 60%).

3.2.3 Imputation

The missing data are imputed using the mice and miceadds packages (van Buuren and Groothuis-Oudshoorn 2011; Robitzsch and Grund 2021) with 20 imputations drawn after 10 iterations. In doing so, we use predictive mean matching with dimensionality reduction of the predictor space through a partial-least squares regression (Robitzsch et al. 2016). We opt for this method because it can deal with a sample size of 2000 without dropping some of the many potentially relevant predictor variables from imputation models. Correspondingly, this approach has shown to perform comparatively well with the data at hand compared to alternative techniques, such as logistic regression models and classification and regression trees (Axenfeld et al. 2022b).

3.2.4 Estimation

4 Results

4.1 Univariate frequencies

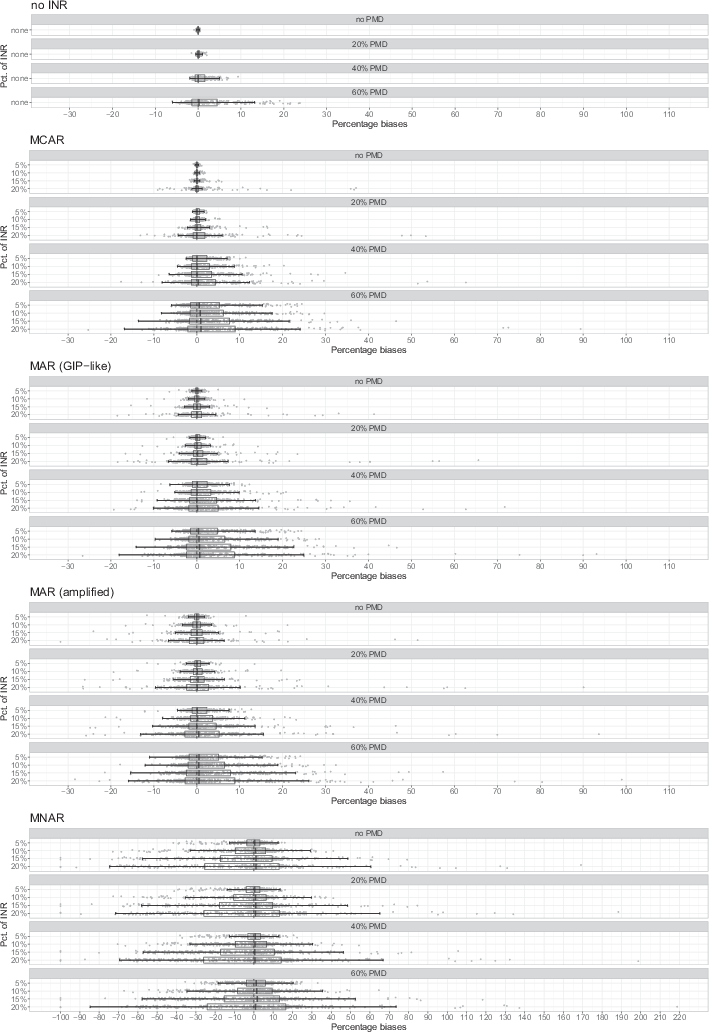
Fig. 1 displays the percentage MC biases averaged over all simulation runs for each univariate frequency estimate (displayed on the x axis) under the different INR and PMD scenarios. Each of the displayed data points refers to the average bias of one specific category of a variable. To simplify the analysis, boxplots are drawn over the average biases. For each mechanism, Fig. 1 shows several of these plots referring to the percentage biases obtained with different proportions of INR and PMD. In addition, the exact numbers for the percentage biases discussed below are displayed in an appendix (Table B.1).

Fig. 1 Average percentage Monte Carlo biases of univariate frequency estimates for 285 categories of 44 variables, by response mechanism and proportions of item nonresponse and planned missing data

, depending on the size of the frequency (1∕θ− 1). Thus, the phenomenon that Fig. 1 tends to depict more pronounced percentage biases in the positive than in the negative results from their calculation and represents no finding in itself.

The first boxplot in Fig. 1 depicts percentage MC biases when no missing data at all occurs (and consequently, no data are imputed). Correspondingly, all biases are approximately zero. The following three boxplots show the percentage MC biases for 20, 40, and 60% PMD (still without INR). We can observe biases increasing with increasing shares of PMD, even without INR: The central 50% of biases (that is, 25% of biases are smaller and another 25% are larger) still concentrate at about 0% with 20% PMD, range from −1% to

with 40% PMD, and from −1% to

with 60% PMD.

The plots beneath show the results for 5, 10, 15, and 20% INR that is MCAR, again separately for 0, 20, 40, and 60% PMD. Each of these INR scenarios replicates the finding that percentage MC biases increase with more PMD. Similarly, it also shows that biases increase with the proportion of INR despite the MCAR mechanism. With 60% PMD, for example, the central 50% of biases range from −1% to

when there is no INR, from −1% to

with 5% INR, from −2% to

with 10% INR, from −2% to

with 15% INR, and from −2% to

with 20% INR. In comparison to the scenarios without INR, we also observe that percentage biases for a few categories take extreme values. This is because the prevalence of INR varies heavily between variables. For example, in the most extreme scenario (60% PMD and 20% INR), three extreme outliers with percentage biases of each more than 70% stand out. These refer to categories at the tails of the variables CE38256 and CE38260, which have the highest proportions of INR (in the scenario with 20% INR and 60% PMD 68% of cases are unobserved).

The subsequent plots show the results for INR that is MAR and as frequent as in the GIP or according to the amplified mechanism. The general patterns observed before recur in both scenarios: Percentage MC biases increase with larger proportions of both PMD and INR. Yet, INR appears to cause somewhat larger biases under MAR than under MCAR, especially with the amplified MAR mechanism. In the 20% INR scenario with no PMD, for instance, the central 50% of biases range from −1% to

for the GIP-like MAR mechanism and from −2% to

for the amplified MAR mechanism while concentrating at about 0% for the MCAR mechanism. Interestingly, the presence of PMD (although in general yielding increased biases) seems to attenuate the effect of the INR mechanism to some extent: In the most extreme scenario with 60% PMD and 20% INR, the central 50% of percentage biases range from −2% to

under both MCAR and GIP-like MAR, and from −3% to

under amplified MAR. Hence, under 60% PMD and 20% INR the amplified MAR mechanism increases the range of the central 50% of biases by only 1 percentage point⁴ compared to MCAR, as opposed to 3 percentage points under 0% PMD and 20% INR.

For INR that is MNAR (displayed in the bottom of Fig. 1), we observe a different pattern. The percentage MC biases generally are much larger than under MCAR or MAR (note that the scale of the x axis for MNAR differs from the rest because otherwise, many biases would fall out of display range). For example, the central 50% of biases with 40% PMD and 20% INR range from −26% to

under MNAR, as opposed to −3% to

under amplified MAR, −2% to

under GIP-like MAR, and −1% to

under MCAR. In consequence, we observe some extreme cases with larger proportions of INR (15 and 20%), with some frequencies being biased upwards by more than

. This indicates that some categories of variables are not observed at all throughout the simulation due to the MNAR mechanism.

Due to the large effect of the INR under MNAR, the proportion of PMD affects the accuracy of estimates less than under the other mechanisms. With 10% INR, for example, the central 50% of percentage MC biases range from −10% to

both when there is no PMD or with 20% PMD, from −10% to

with 40% PMD, and from −8% to

with 60% PMD.

4.2 Bivariate correlations

Fig. 2 shows the results for the average percentage MC biases of bivariate Spearman correlations that are larger than 0.2 in the population data. In doing so, it follows the same structure as Fig. 1. Here, each data point refers to the Monte Carlo bias of the correlation of one variable pair. Unlike Fig. 1, 2 also covers values below −100%, as correlations can be both positive and negative. Again, exact numbers for the percentage biases are also displayed in the appendix (Table B.2).

Fig. 2 Average percentage Monte Carlo biases of bivariate Spearman correlation estimates for 88 variable pairs correlated by 0.2 or more in the population data, by response mechanism and proportions of item nonresponse and planned missing data

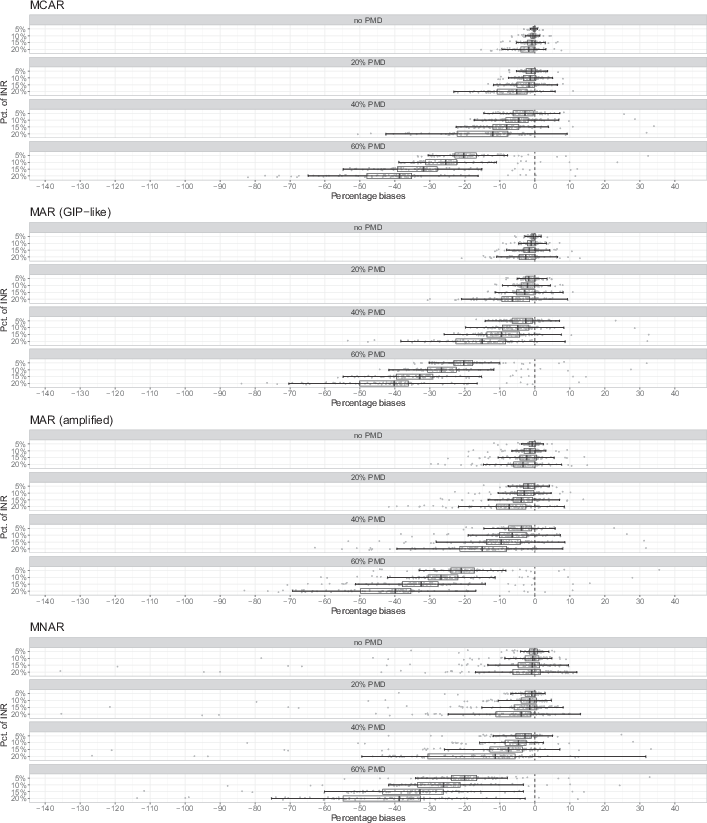
As for the univariate frequencies, we can observe percentage MC biases increase with increasing proportions of PMD, with a clear tendency towards underestimating relationships between variables. This effect is especially severe for the scenario with the highest share of PMD: Considering the scenarios without INR, the central 50% of biases range from −2% to 0% with 20% PMD, from −5% to 0% with 40% PMD, and from −18% to −12% with 60% PMD. Thus, the results are slightly different for frequencies and correlations: Given large proportions of PMD, almost all correlations are considerably biased downwards, while at least some frequencies still have percentage biases close to zero (see Fig. 1).

Again, increasing proportions of INR also yield increasing percentage MC biases, even under MCAR. For each of the INR mechanisms, the largest biases emerge when the proportions of both PMD and INR is high. For example, with 60% PMD and 20% INR that is MCAR, the central 50% of biases range from −48% to −35%, as opposed to from −18 to −12% with 60% PMD but no INR. This means that biases are roughly doubled in size despite the total proportion of missing data increases only from 60 to 68% (see Table 1).

We also observe that MC biases under MAR are similar to those under MCAR, with only minimal tendency towards increasing percentage MC biases when the INR is MAR (GIP-like or amplified, respectively) as compared to MCAR. However, the differences are much less pronounced as with the frequency estimates. With 20% INR and 40% PMD, for example, the central 50% of biases range from −21% to −8% under amplified MAR and from −23% to −8% under the GIP-like MAR, as opposed to −22% to −8% under MCAR.

For INR that is MNAR, we again observe some tendency towards larger percentage MC biases compared to both the MCAR and MAR scenarios. With 20% INR and no PMD, for example, the central 50% of biases range from −6% to

under MNAR, as opposed to −6% to 0% under amplified MAR, −5% to 0% under GIP-like MAR, and −4% to 0% under MCAR. However, this effect is less pronounced and less clear than with the frequency estimates. There also tend to be more MC biases in the area around zero than under the MAR scenarios. This suggests that in this simulation study, MNAR affects some correlations considerably while leaving others largely intact. Apart from that, we again observe some extreme biases exceeding −100% with 15 or 20% INR that is MNAR, implying that the direction of these relationships reverses systematically due to the INR. These extreme biases occur primarily in the correlation of the variables BG38001 and BG38002, which have the strongest variability in nonresponse propensities throughout all variables due to their good nonresponse-model fit in the preliminary analysis.

Compared to the results on univariate frequencies, the proportion of PMD exhibits a larger effect on the accuracy of correlations under MNAR. With 20% INR that is MNAR, for example, the central 50% of percentage MC biases range from −6% to

when there is no PMD, from −11% to −1% with 20% PMD, from −31% to −6% with 40% PMD, and from −55% to −33% with 60% PMD.

5 Summary

6 Discussion

The most important limitation is that the study’s findings rely on a simulation based on specific social survey data. Therefore, their external validity may depend on how similar real data-collection scenarios would be to our simulation setup. Through relying on real social survey data and the INR observed in this dataset, we attempted to create a realistic environment. We modelled INR separately for each item based on the other variables in the dataset using linear additive effects. However, INR in the real world could work differently. For example, INR could follow non-linear mechanisms (see, for example, Collins et al. 2001) or be the result of interaction effects. In particular, the absence of interaction effects might be responsible for the weaker impact of the modelled nonresponse mechanism on correlations compared to univariate frequencies.

Furthermore, the variables in our dataset were discrete. In continuous variables, by contrast, single outliers could have considerable leverage on correlation estimates. Therefore, MNAR mechanisms in continuous variables might potentially affect correlation estimates more severely than found in this study. Moreover, we treated INR as a single uniform missing-data source. Yet, in real surveys there are different subtypes of INR (e.g., refusals, data collection errors, etc.) that might behave differently regarding their response mechanism (see, for example, Shoemaker et al. 2002). Apart from all that, response mechanisms could also behave differently in surveys on different substantive topics. Therefore, this study should be replicated with different data in the future.

In addition, our study focuses on INR as one of several manifestations of missing data that commonly occur in social surveys. Other important sources of missing data, such as unit nonresponse, were out of scope. However, we encourage future research on how these other missing-data sources in surveys interact with the imputation of PMD.

A final limitation is that we examined the accuracy of univariate and bivariate but not multivariate estimates. Yet, for substantive researchers the performance of multivariate models under different planned missingness scenarios may also be highly relevant. Thus, future research should address this issue as well.

Our findings may also guide future research in several other ways. First of all, they allow some direct conclusions for survey design. In particular, survey designers are recommended to carefully evaluate how much PMD is necessary and not introduce more than that, considering that the quality of estimates tends to plummet when the proportion of missing data becomes too large. This is especially the case for items that can be expected to produce considerable amounts of INR. In such items, to allow for an appropriate imputation one may consider reducing the proportion of PMD or allocating them to the core module.

Similarly, it seems particularly important in SQD surveys to keep INR at a low level. For example, this is especially relevant considering the way modules are constructed. For instance, earlier research shows that items of one topic should be allocated to different split-questionnaire forms rather than all to the same in order to support the imputation (Axenfeld et al. 2022a; Imbriano and Raghunathan 2020; Raghunathan and Grizzle 1995). It is still an open empirical question how (and if so, when) this would affect INR rates or response quality in general compared to procedures allocating items of one topic to the same questionnaire form. Therefore, future research should investigate this issue, such that INR can be taken into account when designing split questionnaires.

Interactions between SQDs and the participants’ response behaviour may also play a role in evaluating the costs and benefits of an SQD for a specific survey. By reducing respondent burden in terms of questionnaire length, SQDs are supposed to decrease unit nonresponse, breakoff, and measurement error (Galesic and Bosnjak 2009; Peytchev and Peytcheva 2017) at the cost of additional planned missingness (Graham et al. 1996; Raghunathan and Grizzle 1995; Peytchev and Peytcheva 2017). This notion highlights key empirical questions for survey researchers considering to implement an SQD in a survey: How much PMD is needed to obviate a given amount of unit nonresponse, breakoff, or measurement error? Is the averted nonresponse considered MNAR, or is it MCAR or MAR? For example, on the one hand, if introducing a limited amount of PMD can prevent a considerable amount of unit nonresponse that is MNAR, the benefits of the SQD may outweigh its costs. On the other hand, if large amounts of PMD can inhibit relatively little nonresponse that can also be expected to be MAR, the opposite may be the case. To allow reasonable claims about the expectable usefulness of an SQD for a specific survey, however, our study would need to be replicated with a broad variety of different survey datasets first. Furthermore, experimental research would be needed to investigate if and how different strategies to design split questionnaires affect response behaviour. First evidence on this domain shows differences in respondents’ evaluation of split questionnaires with more versus less frequent switches between topics (Adigüzel and Wedel 2008). Despite the need for more research, this simulation study may provide a first piece of evidence to help researchers assess to what extent an SQD might make sense for a given survey.

1 Supplementary Information

References

Adigüzel, F., & Wedel, M. (2008). Split questionnaire design for massive surveys. Journal of Marketing Research, 45(5), 608–617. a, b

Auguie, B. (2017). “gridExtra: Miscellaneous Functions for ‘Grid’ Graphics.” R package version 2.3. https://CRAN.R-project.org/package=gridExtra →

Axenfeld, J. B., Blom, A. G., Bruch, C., & Wolf, C. (2022a). Split Questionnaire Designs for Online Surveys: The Impact of Module Construction on Imputation Quality. Journal of Survey Statistics and Methodology, 10(5), 1236–1262. a, b, c, d, e

Axenfeld, J. B., Bruch, C., & Wolf, C. (2022b). General-purpose imputation of planned missing data in social surveys: different strategies and their effect on correlations. Statistics Surveys, 16, 182–209. a, b

Bahrami, S., Aßmann, C., Meinfelder, F., & Rässler, S. (2014). A split questionnaire survey design for data with block structure correlation matrix. In U. Engel, B. Jann, P. Lynn, A. Scherpenzeel & P. Sturgis (Eds.), Improving survey methods: lessons from recent research (pp. 368–380). New York: Routledge. →

Bech, M., & Kristensen, M. B. (2009). Differential response rates in postal and Web-based surveys in older respondents. Survey Research Methods, 3(1), 1–6. a, b, c, d

Berinsky, A. E. (2008). Survey non-response. In W. Donsbach & M. W. Traugott (Eds.), The SAGE handbook of public opinion research (pp. 309–321). Thousand Oaks: SAGE. →

Blom, A. G., Gathmann, C., & Krieger, U. (2015). Setting up an online panel representative of the general population: the German Internet panel. Field Methods, 27(4), 391–408. →

Blom, A. G., Bossert, D., Funke, F., Gebhard, F., Holthausen, A., Krieger, U., & SFB 884 “Political Economy of Reforms” Universität Mannheim (2016a). German Internet Panel, Wave 1—Core Study (September 2012). ZA5866 Data file Version 2.0.0. Cologne: GESIS Data Archive. https://doi.org/10.4232/1.12607. →

Blom, A. G., Bossert, D., Gebhard, F., Funke, F., Holthausen, A., Krieger, U., & SFB 884 “Political Economy of Reforms” Universität Mannheim (2016b). German Internet Panel, Wave 13—Core Study (September 2014). ZA5924 Data file Version 2.0.0. Cologne: GESIS Data Archive. https://doi.org/10.4232/1.12619. 

Blom, A. G., Fikel, M., Friedel, S., Höhne, J. K., Krieger, U., Rettig, T., Wenz, A., & SFB 884 “Political Economy of Reforms”, Universität Mannheim (2019a). German Internet Panel, Wave 37—Core Study (September 2018). ZA6957 Data file Version 1.0.0,. Cologne: GESIS Data Archive. https://doi.org/10.4232/1.13390. →

Blom, A. G., Fikel, M., Friedel, S., Höhne, J. K., Krieger, U., Rettig, T., Wenz, A., & SFB 884 “Political Economy of Reforms”, Universität Mannheim (2019b). German Internet Panel, Wave 38 (November 2018). ZA6958 Data file Version 1.0.0. Cologne: GESIS Data Archive. https://doi.org/10.4232/1.13391. 

Blumenberg, C., Zugna, D., Popovic, M., Pizzi, C., Barrios, A. J. D., & Richiardi, L. (2018). Questionnaire breakoff and item nonresponse in web-based questionnaires: multilevel analysis of person-level and item design factors in a birth cohort. Journal of Medical Internet Research, 20(12), e11046. a, b

van Buuren, S. (2018). Flexible imputation of missing data (2nd edn.). Boca Raton: CRC press. a, b, c, d, e

van Buuren, S., & Groothuis-Oudshoorn, K. (2011). mice: Multivariate imputation by chained equations in R. Journal of Statistical Software, 45(3), 1–67. →

van Buuren, S., Brand, J. P., Groothuis-Oudshoorn, C. G., & Rubin, D. B. (2006). Fully conditional specification in multivariate imputation. Journal of Statistical Computation and Simulation, 76(12), 1049–1064. →

Callegaro, M., Lozar, M. K., & Vehovar, V. (2015). Web survey methodology. London: SAGE. →

Callens, M., & Loosveldt, G. (2018). “Don’t know’ responses to survey items on trust in police and criminal courts: a word of caution.” survey methods: insights from the field. https://surveyinsights.org/?p=9237 a, b, c, d, e

Carpenter, J. R., Kenward, M. G., & White, I. R. (2007). Sensitivity analysis after multiple imputation under missing at random: a weighting approach. Statistical Methods in Medical Research, 16(3), 259–275. →

Collins, L. M., Schafer, J. L., & Kam, C. M. (2001). A comparison of inclusive and restrictive strategies in modern missing data procedures. Psychological Methods, 6(4), 330–351. a, b

Copas, A. J., & Farewell, V. T. (1998). Dealing with non-ignorable non-response by using an ’enthusiasm-to-respond’ variable. Journal of the Royal Statistical Society: Series A, 161(3), 385–396. →

Cornesse, C., Felderer, B., Fikel, M., Krieger, U., & Blom, A. G. (2022). Recruiting a probability-based online panel via postal mail: experimental evidence. Social Science Computer Review, 40(5), 1259–1284. →

Durrant, G. B. (2009). Imputation methods for handling item-nonresponse in practice: methodological issues and recent debates. International Journal of Social Research Methodology, 12(4), 293–304. a, b

Elliott, M. N., Edwards, C., Angeles, J., Hambarsoomians, K., & Hays, R. D. (2005). Patterns of unit and item nonresponse in the CAHPS® hospital survey. Health Services Research, 40(6 Pt. 2), 2096–2119. a, b, c

Enderle, T., Münnich, R., & Bruch, C. (2013). On the impact of response patterns on survey estimates from access panels. Survey Research Methods, 7(2), 91–101. a, b

Frick, J. R., & Grabka, M. M. (2005). Item nonresponse on income questions in panel surveys: incidence, imputation and the impact on inequality and mobility. Allgemeines Statistisches Archiv, 89(1), 49–61. →

Friedman, J. H., Hastie, T., & Tibshirani, R. (2010). Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software, 33(1), 1–22. →

Galesic, M., & Bosnjak, M. (2009). Effects of questionnaire length on participation and indicators of response quality in a web survey. Public Opinion Quarterly, 73(2), 349–360. a, b, c

Glynn, R. J., Laird, N. M., & Rubin, D. B. (1986). Selection modeling versus mixture modeling with Nonignorable Nonresponse. In H. Wainer (Ed.), Drawing inferences from self-selected samples (pp. 115–142). New York: Springer. →

Graham, J. W., Hofer, S. M., & MacKinnon, D. P. (1996). Maximizing the usefulness of data obtained with planned missing value patterns: an application of maximum likelihood procedures. Multivariate Behavioral Research, 31(2), 197–218. a, b

Graham, J. W., Taylor, B. J., Olchowski, A. E., & Cumsille, P. E. (2006). Planned missing data designs in psychological research. Psychological Methods, 11(4), 323–343. →

Heckman, J. J. (1976). The common structure of statistical models of truncation, sample selection and limited dependent variables and a simple estimator for such models. Annals of Economic and Social Measurement, 5(4), 475–492. →

Imbriano, P. M., & Raghunathan, T. E. (2020). Three-form split questionnaire design for panel surveys. Journal of Official Statistics, 36(4), 827–854. a, b

Klein, D. J., Elliott, M. N., Haviland, A. M., Saliba, D., Burkhart, Q., Edwards, C., & Zaslavsky, A. M. (2011). Understanding nonresponse to the 2007 medicare CAHPS survey. The Gerontologist, 51(6), 843–855. a, b, c, d

Kmetty, Z., & Stefkovics, A. (2021). Assessing the effect of questionnaire design on unit and item-nonresponse: evidence from an online experiment. International Journal of Social Research Methodology, 25(5), 659–672. →

de Leeuw, E. (2008). Self-administered questionnaires and standardized interviews. In P. Alasuutari (Ed.), Handbook of social research methods (pp. 313–327). London: SAGE. →

de Leeuw, E. D., Hox, J., & Huisman, M. (2003). Prevention and treatment of item nonresponse. Journal of Official Statistics, 19(2), 153–176. a, b, c

Little, R. J. A. (2009). Selection and pattern-mixture models. In G. M. Fitzmaurice, M. Davidian, G. Verbeke & G. Molenberghs (Eds.), Longitudinal data analysis (pp. 409–431). Boca Raton: CRC Press. →

Little, R. J. A., & Rubin, D. B. (2020). Statistical analysis with missing data (3rd edn.). Hoboken: Wiley. a, b

Luijkx, R., Jónsdóttir, G. A., Gummer, T., Stähli, E. M., Fredriksen, M., Reeskens, T., Ketola, K., Brislinger, E., Christmann, P., Gunnarsson, S. Þ., Hjaltason, Á. B., Joye, D., Lomazzi, V., Maineri, A. M., Milbert, P., Ochsner, M., Pollien, A., Sapin, M., Solanes, I., Verhoeven, S., & Wolf, C. (2021). The European values study 2017: on the way to the future using mixed-modes. European Sociological Review, 37(2), 330–346. →

Meitinger, K., & Johnson, T. P. (2020). Power, culture and item nonresponse in social surveys. In P. S. Brenner (Ed.), Understanding survey methodology: sociological theory and applications (pp. 169–191). Cham: Springer. a, b, c, d

Messer, B., Edwards, M., & Dillman, D. (2012). Determinants of item nonresponse to web and mail respondents in three address-based mixed-mode surveys of the general public. Survey Practice. https://doi.org/10.29115/SP-2012-0012. a, b, c, d, e

Microsoft, & Weston, S. (2020). “foreach: provides Foreach looping construct.” R package version 1.5.0 →

Montagni, I., Cariou, T., Tzourio, C., & González-Caballero, J.-L. (2019). ‘I don’t know‘, ‘I’m not sure‘, ‘I don’t want to answer‘: a latent class analysis explaining the informative value of nonresponse options in an online survey on youth health. International Journal of Social Research Methodology, 22(6), 651–667. →

Munger, G. F., & Loyd, B. H. (1988). The use of multiple matrix sampling for survey research. The Journal of Experimental Education, 56(4), 187–191. →

OECD (2014). PISA 2012 technical report. Paris: OECD. →

Peytchev, A., & Peytcheva, E. (2017). Reduction of measurement error due to survey length: evaluation of the split questionnaire design approach. Survey Research Methods, 11(4), 361–368. a, b, c

R Core Team (2021). R: a language and environment for statistical computing. Vienna: R Foundation for Statistical Computing. →

Raghunathan, T. E., & Grizzle, J. E. (1995). A split questionnaire survey design. Journal of the American Statistical Association, 90(429), 54–63. a, b, c, d, e

Rässler, S., & Riphahn, R. T. (2006). Survey item nonresponse and its treatment. Allgemeines Statistisches Archiv, 90(1), 217–232. a, b, c

Robitzsch, A., & Grund, S. (2021). “miceadds: some additional multiple imputation functions, especially for ’mice’.” R package version 3.10–28. https://CRAN.R-project.org/package=miceadds →

Robitzsch, A., Pham, G., & Yanagida, T. (2016). Fehlende Daten und Plausible Values. In S. Breit & C. Schreiner (Eds.), Large-Scale Assessment mit R: Methodische Grundlagen der Österreichischen Bildungsstandardüberprüfung [Methodological Foundation of Standard Achievement Testing] (pp. 259–293). Vienna: facultas. →

Rubin, D. B. (1976). Inference and missing data. Biometrika, 63(3), 581–592. →

Rubin, D. B. (1987). Multiple imputation for nonresponse in surveys. New York: Wiley. a, b, c, d

Shoemaker, D. M. (1973). Principles and procedures of multiple matrix sampling. Cambridge: Ballinger. →

Shoemaker, P. J., Eichholz, M., & Skewes, E. A. (2002). Item nonresponse: distinguishing between don’t know and refuse. International Journal of Public Opinion Research, 14(2), 193–201. a, b

Signorell, A., Aho, K., Alfons, A., Anderegg, N., Aragon, T., Arachchige, C., Arppe, A., Baddeley, A., Barton, K., Bolker, B., Borchers, H. W., Caeiro, F., Champely, S., Chessel, D., Chhay, L., Cooper, N., Cummins, C., Dewey, M., Doran, H. C., Dray, S., Dupont, C., Eddelbuettel, D., Ekstrom, C., Elff, M., Enos, J., Farebrother, R. W., Fox, J., Francois, R., Friendly, M., Galili, T., Gamer, M., Gastwirth, J. L., Gegzna, V., Gel, Y. R., Graber, S., Gross, J., Grothendieck, G., Harrell, F. E. Jr, Heiberger, R., Hoehle, M., Hoffmann, C. W., Hojsgaard, S., Hothorn, T., Huerzeler, M., Hui, W. W., Hurd, P., Hyndman, R. J., Jackson, C., Kohl, M., Korpela, M., Kuhn, M., Labes, D., Leisch, F., Lemon, J., Li, D., Maechler, M., Magnusson, A., Mainwaring, B., Malter, D., Marsaglia, G., Marsaglia, J., Matei, A., Meyer, D., Miao, W., Millo, G., Min, Y., Mitchell, D., Mueller, F., Naepflin, M., Navarro, D., Nilsson, H., Nordhausen, K., Ogle, D., Ooi, H., Parsons, N., Pavoine, S., Plate, T., Prendergast, L., Rapold, R., Revelle, W., Rinker, T., Ripley, B. D., Rodriguez, C., Russell, N., Sabbe, N., Scherer, R., Seshan, V. E., Smithson, M., Snow, G., Soetaert, K., Stahel, W. A., Stephenson, A., Stevenson, M., Stubner, R., Templ, M., Lang, T. D., Therneau, T., Tille, Y., Torgo, L., Trapletti, A., Ulrich, J., Ushey, K., VanDerWal, J., Venables, B., Verzani, J., Villacorta Iglesias, P. J., Warnes, G. R., Wellek, S., Wickham, H., Wilcox, R. R., Wolf, P., Wollschlaeger, D., Wood, J., Wu, Y., Yee, T., & Zeileis, A. (2020). “DescTools: Tools for descriptive statistics.” R package version 0.99.36. https://cran.r-project.org/package=DescTools →

Thomas, N., Raghunathan, T. E., Schenker, N., Katzoff, M. J., & Johnson, C. L. (2006). An evaluation of matrix sampling methods using data from the National Health and Nutrition Examination Survey. Survey Methodology, 32(2), 217–231. →

Tourangeau, R., & Yan, T. (2007). Sensitive questions in surveys. Psychological Bulletin, 133(5), 859–883. →

Venables, W. N., & Ripley, B. D. (2002). Modern applied statistics with S. New York: Springer. →

Weston, S. (2017). “doMPI: foreach parallel adaptor for the Rmpi package.” R package version 0.2.2. https://cran.r-project.org/package=doMPI →

Wickham, H. (2016). ggplot2: elegant graphics for data analysis. New York: Springer. →

Wickham, H., & Miller, E. (2019). “haven: Import and Export ’SPSS’, ’Stata’ and ’SAS’ Files.” R package version 2.1.1. https://CRAN.R-project.org/package=haven →

Wickham, H., François, R., Henry, L., & Müller, K. (2021). “dplyr: A Grammar of Data Manipulation.” R package version 1.0.7. https://CRAN.R-project.org/package=dplyr →

Yan, T., Curtin, R., & Jans, M. (2010). Trends in income nonresponse over two decades. Journal of Official Statistics, 26(1), 145–164. →

Yu, H. (2002). Rmpi: parallel statistical computing in R. R News, 2(2), 10–14. →

Zou, H., & Hastie, T. (2005). Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 67(2), 301–320. →